Понятие - инвариантность
Cтраница 1
Понятие инвариантности и инвариантов буквально пронизывает точные науки. Думается, что здесь нет необходимости приводить примеры инвариантов в различных разделах современной математики и физики, отметим лишь, что важность понятия инвариантности обусловлена тем, что с его номощью можно выделить такие величины, которые характеризуют внутренние свойства исследуемого объекта. [1]
Понятию инвариантности соответствует более слабое понятие инвариантности в терминах интегралов и в терминах вероятностей. [2]
Введя понятие инвариантности, мы можем сказать: чтобы тот или иной закон не изменил своей формы при переходе от одной инерциальной системы отсчета к другой и, таким образом, удовлетворял принципу относительности Галилея, он должен быть инвариантным к преобразованию Галилея. Этим устанавливается важная роль, отводимая преобразованиям как инструменту, позволяющему установить правильность того или иного закона. В противном случае закон является ошибочным и подлежит уточнению или изменению. [3]
Воспользовавшись понятием инвариантности, прин цип относительности Галилея можно сформулировать следующим образом: уравнения механики инвариантны, по отношению к преобразованиям Галилея. [4]
Понятию инвариантности соответствует более слабое понятие инвариантности в терминах интегралов и в терминах вероятностей. [5]
В связи с этим исключительно важное значение приобретает понятие инвариантности. [6]
Иными словами, для успешного применения к канторовой пыли понятия инвариантности при сдвигах следует весьма значительно ослабить требования этой инвариантности, однако при низкой лакунарности пыли можно обойтись гораздо меньшим ослаблением. [7]
ТАУ применительно к объектам управления, записанным в форме Коши, было введено понятие инвариантности. [8]
В 1939 году Г. В. Щипановым [81] в практику автоматического управления применительно к объектам управления, записанным в форме Коши, было введено понятие инвариантности. [9]
В конце главы 22 мы пришли к выводу, что применить к фракталам инвариантность при сдвигах и космологический принцип возможно, если фракталы сделать случайными, а понятие инвариантности переформулировать к условному виду. Эта переформулировка, собственно, и является главной причиной введения случайных фракталов. [10]
Замечание 2.1. Отметим, что введенные понятия псевдоустойчивости не зависят от того, является ли множество М замкнутым или же компактным или нет. Связь понятий положительной инвариантности, а также свойства быть открытым или замкнутым множеством с понятием псевдоустойчивости устанавливается ниже. [11]
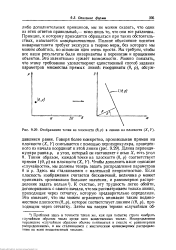 |
Отображение точки на плоскости ( 9, р в линию на плоскости ( X, Y. [12] |
Принцип, к которому приходится обращаться при таких обстоятельствах, называется инвариантностью. Полное объяснение понятия инвариантности требует экскурса в теорию меры, без которого мы можем обойтись, но основная идея очень проста. Мы требуем, чтобы все наши результаты были инвариантны к переносам и вращениям объектов. Это значительно сужает возможности. [13]
Понятие инвариантности и инвариантов буквально пронизывает точные науки. Думается, что здесь нет необходимости приводить примеры инвариантов в различных разделах современной математики и физики, отметим лишь, что важность понятия инвариантности обусловлена тем, что с его номощью можно выделить такие величины, которые характеризуют внутренние свойства исследуемого объекта. [14]
 |
Структурная схема системы комбинированного управления. [15] |
Страницы: 1 2