Понятие - момент - инерция
Cтраница 1
Понятие момента инерции тоже легко обобщается на случай ббльшего числа измерений. [1]
Понятие момента инерции или центробежного момента инерции теряет здесь в известной степени свое значение, так как для них безразлично положение заделки и имеет значение лишь положение дуги в плоскости приложения силы. Напротив того, следует отметить, что одновременное действие изгибающих и крутящих моментов в пространственно нагруженной дуге вызывает различный результат в зависимости от того, к какому концу дуги приложена сила или плечо момента и какой конец рассматривается как защемленный. [2]
Понятие момента инерции было введено нами при рассмотрении вращения твердого тела. Однако следует иметь в виду, что эта величина существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси, подобно тому как тело обладает массой независимо от того, движется оно или находится в покое. [3]
Так возникло понятие момента инерции плоской фигуры. [4]
В выражении (17.5) удобно ввести понятие момента инерции площади поперечного сечения стержня. [5]
В дальнейшем мы рассмотрим обобщение понятия момента инерции для тел произвольной формы и произвольного распределения массы. [6]
Решим два примера для иллюстрации понятия момента инерции и техники его вычисления в простых случаях. [7]
При изучении вращения твердого тела пользуются понятием момента инерции. [8]
В выражении ( 17 5) удобно ввести понятие момента инерции площади поперечного сечения стержня. [9]
Голландский ученый Гюйгенс ( 1629 - 1695) ввел понятие момента инерции, создал теорию маятника, изобрел часы. [10]
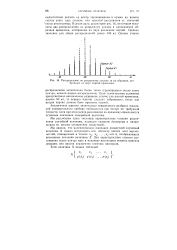 |
Распределение по разрывному усилию ( в кг образцов, отобранных из двух партий проволоки. [11] |
Для характеристики степени рассеивания около центра масс в механике используют понятие момента инерции; оно вполне аналогично понятию дисперсии. [12]
Геометрия масс. В основе геометрии масс абсолютно твердого тела лежит понятие момента инерции тела вокруг некоторой оси. [13]
Строго говоря, при исследовании пространственных систем с дуговыми элементами понятия моментов инерции, центробежных моментов инерции и статических моментов могут применяться лишь из-за наглядности этих понятий, хотя скрывающиеся за ними величины численно и не совпадают точно с геометрическими моментами инерции. [14]
Дополнительно к понятиям осевых и центробежных моментов инерции ( см. § 1.8) введем понятия моментов инерции относительно плоскости и полюса. [15]
Страницы: 1 2