Понятие - центр
Cтраница 2
Для характеристики статической устойчивости часто вводят понятие центра давления. Под центром давления понимают некоторую точку на выбранной оси, через которую проходит равнодействующая аэродинамических сил. [16]
Следует, однако, отметить, что понятие центра инерции отлично от понятия центра тяжести. [17]
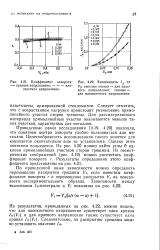 |
Коэффициент поворота. [ IMAGE ] Зависимость / от. [18] |
Проведенные ранее исследования [4.19, 4.20] показали, что понятием центра поворота удобно пользоваться для металлов. Целесообразность использования такого понятия для композитов окончательно еще не установлена. Однако этим понятием пользуются. Из рис. 4.20 можно найти углы Э наклона прямолинейных участков сторон трещины. [19]
Понятие центра масс является более общим, чем понятие центра тяжести: в отличие от понятия центра тяжести понятие центра масс не связано с наличием однородного гравитационного поля. [20]
Понятие центра масс является более общим, чем понятие центра тяжести, так как оно не ограничено одним определенным типом сил, действующих на элементы тела. [21]
 |
Диаграмма напряжение - [ IMAGE ] Модель распространения.| Определение центра поворота. [22] |
Для металлов при определении коэффициента раскрытия трещины COD используют понятие центра поворота. [23]
В более поздних заметках он связывает правило рычага с понятием центра тяжести тела или системы тел, обнаруживая глубокое знакомство с архимедовской теорией равновесия плоских фигур. [24]
Это заключение очень важно, так как оно позволяет распространить понятие центра тяжести на системы невесомые. Эту точку, которую Эйлер предложил называть центром инерции), продолжают часто называть центром тяжести, несмотря на то, что соображения, приводящие к понятию центра тяжести, не применимы к рассматриваемым вопросам. [25]
Такой характер поля, действующего на частицу, вполне строго определяет понятие центра равновесия и ячейки. [26]
При несимметричном размещении диафрагм расчет на горизонтальные нагрузки проводится с использованием понятия центра жесткости. [27]
Отметим, что определение (6.6) совпадает с известным из школьного курса физики понятием центра тяжести. [28]
Мы приведем два определения выпуклости: первое и более распространенное из них основано на понятии центра тяжести, второе двойственно ему. Пока эквивалентность этих двух определений не будет доказана, мы будем пользоваться первым. Оба определения по существу принадлежат Минковскому, а их эквивалентность составляет суть одного из мощных средств анализа, называемого ныне теорема Хана - Банаха; пропагандируемое нами новое название - принцип продолжения. К сожалению, доказательство этого принципа далеко не элементарно: оно требует использования трансфинитной индукции. С этим методом, заменяющим обычную математическую индукцию, сталкивается в наши дни каждый, кто по-настоящему изучает математику. Трансфинитная индукция основана на аксиоме выбора, без которой в анализе мало что можно сделать. [29]
Чтобы распространить на сферическую геометрию содержание упражнения 260 планиметрии, необходимо найти в сферической геометрии аналог понятия центра подобия двух окружностей на плоскости. [30]
Страницы: 1 2 3