Квантовомеханический анализ
Cтраница 1
Квантовомеханический анализ показывает, ja &-NQC уществлен ие. [1]
Квантовомеханический анализ этой задачи несколько ослабляет данное условие. [2]
 |
Диаграмма энергетических JM-M. [3] |
Квантовомеханический анализ показывает, что константы скорости индуцированных переменным электромагнитным полем перехо-дов () - ( -) и ( -) - () равны ( ki k2 k) что они пропорциональны квадрату амплитуды переменного поля. Рост мощности переменного поля увеличи-вает скорость как () - ( - ), так и ( -) - - () переходов. [4]
Квантовомеханический анализ показывает, что константы скорости индуцированных переменным электромагнитным полем переходов С () - ( -) и С ( -) - - () равны ( k k2 k) и что они пропорциональны квадрату амплитуды переменного поля. Рост мощности переменного поля увеличивает скорость обоих переходов. [5]
Квантовомеханический анализ показывает, что константы скорости индуцированных переменным электромагнитным полем переходов () - ( -) и ( -) - () равны ( ki k2k) и что они пропорциональны квадрату амплитуды переменного поля. Рост мощности переменного поля увеличи-вает скорость как () - - ( -), так и ( -) - () переходов. [6]
Эмпирический квантовомеханический анализ Н3 был проведен Эйрингом и Поляни [6] и другими. [7]
 |
Структура энергетических зон в металле ( а, собственном полупроводнике ( б и изоляторе ( в. В заштрихованных участках все уровни заняты электронами. [8] |
Квантовомеханический анализ поведения электрона в периодическом электрическом поле, создаваемом правильно расположенными атомами кристаллической решетки, показывает, что электроны в кристалле могут обладать только некоторыми строго определенными значениями энергии. На энергетической диаграмме эти значения оказываются сгруппированными в полосы, характеризующие диапазоны энергии, которую может иметь электрон в кристалле. Внутри каждой разрешенной зоны энергетические уровни расположены практически непрерывно. Это означает, что даже при очень низких температурах и в самых слабых электрических полях электроны легко возбуждаются и переходят на свободные уровни данной зоны. Но для перехода из одной разрешенной зоны в другую, соответствующую более высокой энергии, электрон должен получить энергию, по крайней мере равную ширине запрещенной зоны. [9]
Квантовомеханический анализ циклотронного резонанса исходит из рассмотрения распределения энергетических уровней кристалла. При отсутствии внешнего магнитного поля электроны в зоне проводимости могут находиться в любом состоянии, относящемся к квазиконтинимуму разрешенных энергий, и никакие из этих электронов не обладают преимущественным поглощением. [10]
Простой и убедительный квантовомеханический анализ Щ можно осуществить с использованием волновой ls - функции для атома водорода в его нормальном состоянии. На -; кривая, показанная пунктиром на рис. 6.2, соответствует энергии отталкивания. [11]
Более строгий квантовомеханический анализ опытов по ( р-р) - рассеянию, физическая сущность которого близка к соответствующему анализу для синглетного ( п-р) - рассеяния, показывает, что ядерное ( без кулоновского) взаимодействие двух протонов практически тождественно ядерному взаимодействию аейтрона с протоном в синглетном состоянии. [12]
Квантовомеханический анализ сил взаимодействия ионов показал, что первая зависимость является менее правильной, хотя и представляет собой хорошее приближение при малых г, и что говорит в пользу экспоненциальной зависимости. [13]
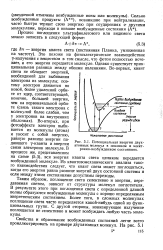 |
Потенциальная энергия двухатомных молекул в основном и электронно-возбужденном состояниях. [14] |
Из квантовомеханического анализа такого взаимодействия следует, что квант света может поглощаться, когда его энергия равна разнице энергий двух состояний системы и если между этими состояниями допустимы переходы. [15]
Страницы: 1 2 3