Замыкание - уравнение
Cтраница 2
Уравнение ( 1 - 10 - 1) является исходным для замыкания уравнений гидродинамики в форме Навье - Стокса. [16]
Формула ( 1 - 10 - 12) является исходной для замыкания уравнений гидродинамики по Трусделлу. [17]
Поскольку уравнения Фридмана - Келлера оказываются всегда незамкнутыми, естественно возникает проблема замыкания уравнений для моментов. Основное-различие в поведении этих двух типов компонент турбулентности состоит в том, что крупномасштабные возмущения существенно зависят от геометрии потока и характера внешних воздействий, в то время как режим мелкомасштабных возмущений оказывается в значительной степени имеющим универсальный характер. Подробному разбору развития двух указанных направлений в теории турбулентности будут посвящены § 2 и 4 настоящего обзора. [18]
Отличный от них подход недавно был развит в 12.14 ], в которой замыкание уравнений основывается на соображениях подобия, аналогичных тем, которые были использованы в теории двумерных течений в пограничном слое, а не на обращении к полю средних скоростей. При таком подходе пограничный слой подразделяется на приземный слой воздуха и внешний пограничный слой. [19]
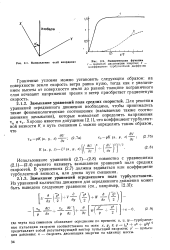 |
Направление осей координат. [20] |
Использование уравнений (2.7) - (2.8) совместно с уравнениями (2.1) - (2.4) принято называть замыканием уравнений поля средних скоростей. В уравнениях (2.7) должны задаваться или коэффициент турбулентной вязкости, или длина пути смешения. [21]
Формулировка задач, описывающих турбулентное течение, является в принципе приближенной, что обусловлено необходимостью замыкания уравнений турбулентного движения посредством дополнительных гипотез. В ряде случаев поставленные таким образом задачи имеют точное решение, что позволяет апробировать принятую гипотезу турбулентности. [22]
В последнее время для расчета турбулентных пограничных слоев в газодинамических устройствах используются новые математические модели, в которых замыкание уравнений производится с помощью дополнительных дифференциальных уравнений вторых моментов, а не конечных алгебраических соотношений типа формулы Прандтля. [23]
После этого производятся операции связывания моделей ( этап 7), предусматривающие определение соответствия количества уравнений и количества зависимых переменных и замыкание уравнений объекта. Преобразование моделей ( этап 8) осуществляется с целью исключения промежуточных переменных и упрощения моделей. На последнем этапе 9 рассчитываются численные коэффициенты модели. Оценивается возможность упрощения уравнений, в том числе их линеаризация. [24]
Последняя представляет собой исчерпывающий трактат по отдельной теме: теория уравнения Больцмана была развита в связи с проблемой вычисления коэффициентов переноса для замыкания уравнений сохранения механики сплошной среды. [25]
Так как число входящих в нелинейные уравнения неизвестных функций преобладает над числом описывающих их уравнений, то проблема турбулентного переноса состоит в замыкании уравнений переноса. [26]
Следующие разделы главы посвящены подробному изложению двух основных методов построения уравнений гидромеханики псевдоожиженного слоя - феноменологического метода и метода осреднения, а также рассмотрению различных гипотез, которые используются для замыкания уравнений гидромеханики. [27]
Для замыкания уравнений математической модели необходимо привлечь дополнительные соотношения взаимодействия частиц со стенками аппарата. [28]
В работе [2.7] сообщается об успешных предсказаниях характеристик пограничного слоя, основывающихся на уравнении (2.9) и различных феноменологических зависимостях; несмотря на это, все еще существуют различные мнения относительно сравнительных достоинств этих зависимостей. В частности, замыкание уравнений осредненного поля турбулентности, по-видимому, дает преимущества при изучении трехмерных течений в пограничном слое атмосферы. [29]
Рассматривается с единых позиций турбулентное горение газов и ряд вопросов теории турбулентно ст. Объединение этих научных дисциплин в рамках одной книги предпринято впервые, и оно достигнуто благодаря широкому использованию плотностей распределений вероятностей концентраций, скорости и других величин в турбулентных потоках. Систематизированы методы вывода и замыкания уравнений для распределений вероятностей, значительное внимание уделено описанию перемежаемости. Исследуется ряд проблем горения неперемешанных газов и горения однородной горючей смеси. [30]
Страницы: 1 2 3