Линейный регрессионный анализ

Cтраница 1

Линейный регрессионный анализ подтверждает выдвинутую гипотезу о соответствии рассматриваемого периода этапу выведения на рынок, так как темпы роста сбыта увеличиваются, о чем свидетельствует рост коэффициента при переменной ( at) по периодам от начала жизненного цикла. [1]

Характеристики линейных моделей выручки от реализации. [2]

Линейный регрессионный анализ подтверждает выдвинутую гипотезу о соответствии рассматриваемого периода этапу выведения на рынок, так как темпы роста сбыта увеличиваются, о чем свидетельствует рост коэффициента при переменной ( а) по периодам от начала жизненного цикла. [3]

Линейный регрессионный анализ - это математический метод, используемый для вывода линейного уравнения совокупных затрат: у а Ьх, где у - совокупные затраты; а - постоянные затраты; Ъ - удельные переменные затраты; х - объем деятельности. [4]

Линейный регрессионный анализ математически более точен, чем анализ счетов, график разброса и анализ диапазона. Однако он предполагает поведение затрат только линейным; математическая точность не обязательно дает более точный прогноз затрат. [5]

Линейный регрессионный анализ данных, приведенных на рис. 5, показал, что кинетическая диаграмма описывается двумя линейными участками. [6]

Задача линейного регрессионного анализа ( метода наименьших квадратов) состоит в том, чтобы, зная положение точек 1 - 8 на. [7]

Задача линейного регрессионного анализа ( метода наименьших квадратов) состоит в том, чтобы, зная положение точек 1 - 8 на плоскости, так провести линию регрессии, чтобы сумма квадратов отклонений Д / вдоль оси Оу ( ординаты) этих точек U от проведенной прямой была минимальной. [8]

Применение линейного регрессионного анализа эффективно при статистической обработке результатов усталостных испытаний в области ограниченной выносливости. [9]

В линейном регрессионном анализе прошлых затрат значение, рассчитанное для коэффициента а, представляет собой удельные переменные затраты. [10]

Статистическая теория линейного регрессионного анализа является фундаментом многих разделов теории планирования эксперимента. В данной главе основные положения линейного регрессионного анализа подробно объясняются и обосновываются. Лицам, знакомым с теорией линейного регрессионного анализа, достаточно лишь бегло просмотреть главу с целью ознакомления с используемыми далее понятиями и обозначениями. [11]

Таким образом, современный линейный регрессионный анализ позволяет обрабатывать практически любые промысловые данные, встречающиеся в практике бурения. [12]

Следовательно, задача линейного регрессионного анализа ( метода наименьших квадратов) состоит в том, чтобы сумма квадратов отклонений SQ экспериментальных точек ( xt, yt) вдоль ординаты от проведенной прямой была минимальной. [13]

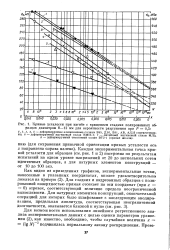Кривые усталости при изгибе с вращением гладких полированных образцов диаметром 8 - 12 мм для вероятности разрушения при Р 0 5. [14]

Для возможности использования линейного регрессионного анализа экспериментальных данных с целью оценки параметров уравнения ( 2), как известно, необходимо, чтобы случайная величина х ( lg N) - 2 подчинялась нормальному закону распределения. [15]

Страницы: 1 2 3 4