Конвективный вал
Cтраница 1
Устойчивость конвективных валов к возмущениям, разнообразной структуры в широком диапазоне чисел Рэлея и Прандтля будет рассмотрена в разд. [1]
Тенденция конвективных валов выстраиваться вблизи боковых стенок перпендикулярно им - сейчас хорошо известный экспериментальный факт. Но здесь необходимо сделать три важные оговорки. [2]
 |
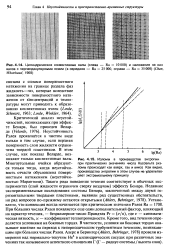
К структуре неустойчивости пространственно-периодических движений. изображены линии постоянной фазы. Моды неустойчивости. а Экхауза, б зигзаго-вая, в типа косых уширений. [3] |
Эту моду по аналогии с неустойчивостью конвективных валов в горизонтальном слое ( см. § 36) можно назвать зигзаговой. [4]
Аналитически можно получить лишь решение в виде стационарных конвективных валов, все прочие режимы можно исследовать только приближенно или численно. [5]
При подогреве снизу в полости формируются короткие отрезки конвективных валов, упирающиеся своими торцами в длинные стенки канала ( этот эффект будет обсужден в разд. В результате исключаются эффекты, связанные с трехмерными деформациями валов, и изучать динамику волновых чисел такого простого валикового течения особенно удобно. Но, конечно, результаты опытов с каналами могут соответствовать случаю горизонтального слоя лишь качественно, а не количественно. [6]
Численные эксперименты с начальными условиями III типа показывают, что развитый конвективный вал ведет себя как упругий объект. [7]
В опытах на силиконовом масле с мало меняющейся вязкостью наблюдались либо конвективные валы - в закрытом сверху слое, либо шестиугольники - в слое со свободной поверхностью, где действует термокапиллярный эффект. Если же использовался арохлор, вязкость которого сильно зависит от температуры, то шестиугольники возникали и в закрытом слое при условии, что он был достаточно тонким и, соответственно, градиент температуры - достаточно большим. [8]
Дальнейшее развитие метода малого параметра ( применительно к движениям в виде двумерных конвективных валов), содержавшееся в работах [ 14 15 48 ], показало, что с помощью высоких приближений метода удается получить стационарные решения для достаточно высоких значений надкритичности. [9]
В результате нарастания возмущений с различными направлениями волнового вектора могут формироваться пространственно-периодические движения разной структуры ( конвективные валы, прямоугольные и гексагональные ячейки), а также движения, содержащие разного рода структурные дефекты. [10]
Однако следует отметить, что уравнения Лоренца описывают эксперимент Бенара только непосредственно вблизи перехода от теплопереноса к конвективным валам, так как пространственные фурье-коэффициенты, оставленные Лоренцем в системе уравнений, описывают только простые валы. Для описания экспериментально наблюдаемого хаоса необходимо сохранить гораздо больше пространственных фурье-ком-понент. [11]
Неустойчивость Рэлея проявляется в чистом виде только в том случае, если верхняя поверхность слоя жидкости ограничена твердой пластинкой. В этом случае, как показал Веларде, возникают только конвективные валы. [13]
Они применили аппарат, многократно использованный Буссе и его соавторами при исследовании устойчивости конвективных валов, а затем и некоторых трехмерных форм конвекции в условиях сильной нелинейности. [15]
Страницы: 1 2 3