Конвективный вал
Cтраница 2
При малых разностях температур ДГ преобладает вязкость, жидкость покоится и тепло переносится постоянной теплопроводностью. Это состояние становится неустойчивым при критическом значении Ra числа Рэлея R ( пропорционального ДГ, см. приложение 1), и появляются стационарные конвективные валы. С дальнейшим ростом R после второго порога Rc наблюдается переход к хаотическому движению. [16]
Для возмущений же с k k в области k km № и АЯ - положительны. В области kkm, как показывает анализ, сохраняются выводы, полученные в первом приближении, а именно, всегда находятся нарастающие возмущения, приводящие к неустойчивости конвективных валов. [17]
Прежде всего, прямоугольные, гексагональные и другие пространственные структуры оказываются неустойчивыми. Далее, двумерные структуры ( конвективные валы) имеют интервал значений волнового числа, внутри которого они устойчивы. [18]
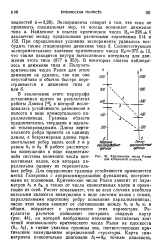 |
Критические числа Рэлея для кубической полости. [19] |
В заключение этого параграфа остановимся кратко на результатах работы Дэвиса [13], в которой исследовалась устойчивость равновесия в полости в виде прямоугольного параллелепипеда. Границы области предполагались твердыми и идеально теплопроводными. В работе рассмотрены возмущения в виде одноэтажной системы конечного числа конвективных валов, оси которых параллельны одному из горизонтальных ребер. Для определения границы устойчивости применяется метод Галеркина с аппроксимирующими функциями, построенными из полиномов. Критическое число Рэлея зависит от пара метров hi и / i2, а также от числа конвективных валов и ориентации их осей. Расчет показывает, что во всех случаях наиболее опасными являются возмущения в виде системы валов с осями, параллельными короткому ребру основания параллелепипеда; число этих валов зависит от соотношения между Л4 и hz и, в общем, возрастает с увеличением этих параметров. Рэлея на плоскости ( hi, hz), a также указаны границы зон, соответствующих кри тическим возмущениям определенной структуры. Карта сим метрична относительно диагонали AiA2; точкам плоскости. [20]
Предельный спучай г О ( отсутствует продольный градиент температуры) соответствует, как уже говорилось, равновесной ситуации в плоском слое с поперечной разностью температур и продольной осью вибрации. Это равновесие теряет устойчивость при критическом значении вибрационного числа Рэлея Rav GruPr; при этом возникает вибрационная конвекция в виде периодической системы конвективных валов. [21]
Соответствующая ( левая) часть диаграммы на рис. 25 иллюстрирует закономерности смены режимов лишь в самых грубых чертах. Детальное описание должно быть весьма конкретным - для резервуара данных размеров и формы и для данных граничных условий на боковых стенках. В то же время устойчивость конечноамплитудной конвекции сильно зависит от общей геометрии течения - это станет ясно из обсуждения закономерностей поведения волновых чисел конвективных валов ( гл. [22]
Обсудим физическую интерпретацию этих результатов. Теоретические выводы о величине реализованного волнового числа были сделаны на основании ключевого предположения, что локально k kc там, где R Rc. Если рассматривать лишь возможность существования стационарных конвективных течений с тем или иным k при данном R в однородной области, то этот шаг с логической стороны сомнителен. Значения Rc и kc были найдены для пространственно-периодических течений в однородном слое, где взаимодействие конвективных валов не создает среднего потока энергии вдоль слоя. В системах с рампом это, вообще говоря, не так: более энергичные валы, находящиеся в области с большей надкритичностью, передают свою энергию менее энергичным, существующим в менее надкритических условиях. Мало того, этот поток энергии не может обращаться в ноль в той самой точке, где режим критический, а неизбежно будет проникать в подкритическую область. [23]
Итак, если внешнее поле произвольно ориентировано относительно слоя, то критическое значение числа Рэлея определяется лишь поперечной к слою ( вертикальной) составляющей внешнего поля. Таким образом, при критическом значении числа Рэлея возможны пространственные возмущения с различным соотношением k и &2. Наличие продольной ( горизонтальной) составляющей магнитного поля снимает это вырождение: наиболее опасные критические возмущения имеют форму конвективных валов, оси которых параллельны продольной составляющей поля. [24]
Для создания возмущений контролируемой формы в опытах использовались решетки, состоящие из параллельных полос. Опыты показали, что при надкритичностях, достигавших 2 5Rm, валы устойчивы, если их волновые числа близки к значению km, соответствующему минимуму нейтральной кривой. Эти эксперименты, как и некоторые другие [ 39 43 ], говорят о том, что если температурная зависимость вязкости мала, то устойчивой формой надкритического движения являются конвективные валы. Обсуждаемые эксперименты представляют интерес также и в другом отношении: они могут служить качественным подтверждением вывода работы Шлютера, Лорца и Буссэ о существовании ( при фиксированном R) подынтервала волновых чисел, соответствующих устойчивым конвективным валам. [25]
Имеется и другой тип режимов конвекции с постоянно присутствующей нестационарностью, который получил название хаоса спиральных дефектов. Авторы экспериментировали с углекислым газом под давлением 32 7 бар ( Р - 0 96) в цилиндрическом резервуаре с Г 78, наружная стенка которого была сделана из фильтровальной бумаги и оказывала очень слабое вынуждающее действие. Такой режим ( скажем, при е к 0 1) нестационарен - для него характерно движение дефектов. При е и 0 4 во внутренней части резервуара конвективные валы начинают образовывать вращающиеся спирали ( рис. 29, в), и при е 0 5 наблюдаются многочисленные взаимодействующие вращающиеся спирали и другие дефекты. Как сказано в работе [187], обычно спираль делала несколько оборотов, сдвигаясь на расстояние, сравнимое с ее диаметром, прежде чем разрушиться или изменить число рукавов. [26]
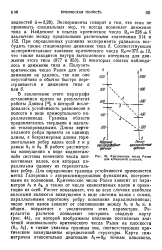 |
Критические числа Рэлея для кубической полости. [27] |
В заключение этого параграфа остановимся кратко на результатах работы Дэвиса [13], в которой исследовалась устойчивость равновесия в полости в виде прямоугольного параллелепипеда. Границы области предполагались твердыми и идеально теплопроводными. В работе рассмотрены возмущения в виде одноэтажной системы конечного числа конвективных валов, оси которых параллельны одному из горизонтальных ребер. Для определения границы устойчивости применяется метод Галеркина с аппроксимирующими функциями, построенными из полиномов. Критическое число Рэлея зависит от пара метров hi и / i2, а также от числа конвективных валов и ориентации их осей. Расчет показывает, что во всех случаях наиболее опасными являются возмущения в виде системы валов с осями, параллельными короткому ребру основания параллелепипеда; число этих валов зависит от соотношения между Л4 и hz и, в общем, возрастает с увеличением этих параметров. Рэлея на плоскости ( hi, hz), a также указаны границы зон, соответствующих кри тическим возмущениям определенной структуры. Карта сим метрична относительно диагонали AiA2; точкам плоскости. [28]
Для создания возмущений контролируемой формы в опытах использовались решетки, состоящие из параллельных полос. Опыты показали, что при надкритичностях, достигавших 2 5Rm, валы устойчивы, если их волновые числа близки к значению km, соответствующему минимуму нейтральной кривой. Эти эксперименты, как и некоторые другие [ 39 43 ], говорят о том, что если температурная зависимость вязкости мала, то устойчивой формой надкритического движения являются конвективные валы. Обсуждаемые эксперименты представляют интерес также и в другом отношении: они могут служить качественным подтверждением вывода работы Шлютера, Лорца и Буссэ о существовании ( при фиксированном R) подынтервала волновых чисел, соответствующих устойчивым конвективным валам. [29]
Страницы: 1 2 3
