Принцип - аргумент
Cтраница 1
Принцип аргумента, в частности формула (4.40), имеет многочисленные приложения. Приведем, например, следующие две теоремы. [1]
Применяя принцип аргумента ( см. § 33), найдем условия, при выполнении которых характеристический, многочлен ( 1) не имеет корней ( нулей) в правой полуплоскости плоскости независимой переменной Я а / со. Если устремить R к бесконечности, то замкнутый контур 4 будет охватывать всю правую полуплоскость плоскости Я, и если при этом в правой полуплоскости характеристический многочлен D ( Я) имеет корни, то эти корни окажутся внутри замкнутого контура. [2]
Применяя принцип аргумента ( см. § 33), найдем условия, при выполнении которых характеристический, многочлен ( 1) не имеет корней ( нулей) в правой полуплоскости плоскости независимой переменной Я а / о. Если устремить R к бесконечности, то замкнутый контур / будет охватывать всю правую полуплоскость плоскости К, и если при этом в правой полуплоскости характеристический многочлен D ( A) имеет корни, то эти корни окажутся внутри замкнутого контура. [3]
Применим принцип аргумента ( см. формулу (6.3) гл. [4]
Из принципа аргумента ( 1161) вытекает следующее предложение. [5]
Из принципа аргумента вытекает следующая теорема, которую мы сформулируем без доказательства. [6]
Из принципа аргумента вытекает правило, называемое иногда критерием устойчивости Михайлова. [7]
Пользуясь принципом аргумента Коши, можно показать, что достаточное условие асимптотической устойчивости, вытекающее из ( 16), может быть определено по истинному характеристическому уравнению на основе критериев Гурвица, Найквиста и других. [8]
С помощью принципа аргумента легко доказывается Теорема Руше. [9]
Ог По принципу аргумента число / V корней этого уравнения равно L Var Arglf ( Zj) - zf ] в предположении, что ZY однократно пробегает r i в положительном направлении. [10]
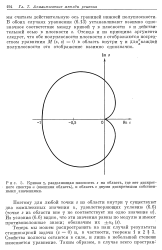 |
Кривая Y разделяющая плоскость s на область, где нет дискретного спектра и ( внешняя область, и область с двумя дискретными собственными значениями. [11] |
Отсюда и из принципа аргумента следует, что обе полуплоскости плоскости z отображаются посредством уравнения М ( z, s) О в область внутри у и для каждой полуплоскости это отображение взаимно однозначно. [12]
Последнее выражение согласно принципу аргумента равно числу нулей функции w - t, в области G. Так как по теореме 1.1 множество f ( D) открыто, то f ( D) G, и теорема доказана. [13]
Последние соотношения выражают так называемый принцип аргумента. Принцип аргумента используется в теории автоматического управления при доказательстве теоремы об устойчивости. [14]
Частотные критерии получаются из принципа аргумента. Поэтому сначала рассмотрим этот принцип. [15]
Страницы: 1 2 3 4