Принцип - максимум - правдоподобие
Cтраница 1
Принцип максимума правдоподобия может рассматриваться [66] как основная идея всех методов и приемов, положенных в основу статистической обработки экспериментальных данных для построения эмпирических зависимостей. В общем виде принцип максимума правдоподобия можно сформулировать так [66]: наилучшее описание явления то, которое дает наибольшую вероятность получить в результате измерений именно те значения, которые и были фактически получены. [1]
Принцип максимума правдоподобия в применении к задачам количественного изучения кинетики формулируется следующим образом. Наилучшими оценками кинетических параметров, соответствующих решению заданной системы уравнений кинетики, являются такие оценки, которые обеспечивают наибольшую вероятность получить в результате подстановки условий эксперимента именно те значения концентраций, которые и были фактически получены. [2]
Принцип максимума правдоподобия может рассматриваться [66] как основная идея всех методов и приемов, положенных в основу статистической обработки экспериментальных данных для построения эмпирических зависимостей. В общем виде принцип максимума правдоподобия можно сформулировать так [66]: наилучшее описание явления то, которое дает наибольшую вероятность получить в результате измерений именно те значения, которые и были фактически получены. [3]
Принцип максимума правдоподобия может рассматриваться [ 6 ( i как основная идея всех методов и приемов, положенных в основу статистической обработки экспериментальных данных для построения эмпирических зависимостей. В общем виде принцип максимума правдоподобия можно сформулировать так [66]: наилучшее описание явления то, которое дает наибольшую вероятность получить в результате измерений именно те значения, которые и были фактически получены. [4]
Принцип максимума правдоподобия может рассматриваться [66] как основная идея всех методов и приемов, положенных в основу статистической обработки экспериментальных данных для построения эмпирических зависимостей. В общем виде принцип максимума правдоподобия можно сформулировать так [66]: наилучшее описание явления то, которое дает наибольшую вероятность получить в результате измерений именно те значения, которые и были фактически получены. [5]
Принцип максимума правдоподобия оказался удивительно удачным. С его помощью найдено большое количество оценок параметров в конкретных ситуациях. [6]
Получаемые с помощью принципа максимума правдоподобия соотношения имеют, конечно, некоторые ошибки. [7]
Нахождение параметров уравнений основано на принципе максимума правдоподобия, согласно которому наилучшими оценками параметров являются те, которые при подстановке в уравнения ( вместе с параметрами процесса в каждой опытной точке) обеспечивают наибольшую сходимость расчетных значений с экспериментальными данными. [8]
Так как в основе указанного метода лежит принцип максимума правдоподобия, то он обеспечивает математически достаточно сильный результат и в рамках выдвинутых предпосылок позволяет получить состоятельную, несмещенную оценку. Однако использование метода в практических ситуациях сильно затруднено из-за жесткости положенных в его основу предпосылок. С позиций экспериментатора случайные величины 8xg и Eg принципиально различны, поскольку оценку 02 дисперсии ошибки измерения 6 % можно получить априори, а оптимальную по своим свойствам оценку дисперсии а можно найти только после проведения полного регрессионного анализа, так так случайная величина гк есть результат действия всех неконтролируемых случайных факторов. [9]
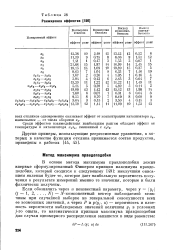 |
Ранжировка эффектов. [10] |
В основе метода максимума правдоподобия лежит впервые сформулированный Фишером принцип максимума правдоподобия, который сводится к следующему [49]: наилучшим описанием явления будет то, которое дает наибольшую вероятность получения в результате измерений именно те значения, которые и были фактически получены. [11]
При использовании метода наименьших квадратов или других норм, основанных на принципе максимума правдоподобия, определение таких интервалов не представляет принципиальных трудностей при известном законе распределения ошибки измерений. [12]
Обычно вырожденное решение не представляет интереса, и мы вынуждены заключить, что принцип максимума правдоподобия не работает для этого класса нормальных смесей. Однако эмпирически установлено, что имеющие смысл решения можно все-таки получить, если мы сосредоточим наше внимание на наибольшем из конечных локальных максимумов функции правдоподобия. Когда мы включаем элементы матрицы 2 1 в элементы вектора параметров в -, мы должны помнить, что только половина элементов, находящихся вне диагонали, независимы. [13]
При нормальном распределении случайных величин метод наименьших квадратов обосновывается в теории вероятностей как частный случай принципа максимума правдоподобия. [14]
Нахождение наилучших оценок коэффициентов регрессии методом регрессионного анализа ( иначе методом наименьших квадратов) соответствует принципу максимума правдоподобия и заключается в решении системы алгебраических уравнений, получае - - м ой приравниванием нулю частных производных 2 ( У - Уоп) 2 по каждому из коэффициентов. [15]
Страницы: 1 2