Принцип - минимальная сложность
Cтраница 2
Теперь задача синтеза систем управления может быть сформулирована в виде следующего принципа, который можно назвать принципом минимальной сложности: среди всех операторов, обладающих заданным уровнем качества, необходимо выбрать оператор минимальной сложности относительно заданной шкалы. [16]
 |
К пояснению сопряженных задач. [17] |
Для систематического выбора сопряженной задачи, решение которой наименее трудоемко, и организации процедуры получения искомого решения можно применить принцип минимальной сложности. [18]
Иными словами, требуется найти экстремум критерия Е ( х, z), где х и z имеют тот же смысл, что и в принципе минимальной сложности. [19]
На этапе функционирования системы, когда структура и характеристики вычислительного комплекса заданы и неизменны, использовать шкалу сложности W ( z) можно в ограниченных пределах. Здесь следует взять шкалу Т ( z) или для повышения эффективности управления использовать сопряженный с принципом минимальной сложности принцип ограниченной сложности. [20]
Рассмотрим общую схему и конкретные алгоритмы синтеза и оптимизации адаптивных логических решающих правил. Принцип минимальной сложности, лежащий в основе их синтеза, обеспечивает простоту реализации и высокую экстраполирующую силу. Благодаря этим качествам адаптивные решающие правила находят все более широкое применение в ГАП, в частности, в РТК адресования деталей на конвейерах. [21]
Первое направление заключается в разработке специальных методов синтеза, ориентированных на получение параллельных структур. Второе - состоит в разработке специальных алгоритмов выполнения операций с матрицами, содержащих цепочки не связанных друг с другом расчетов. В настоящей статье в рамках первого направления предлагается принцип минимальной сложности алгоритмов распознавания-оценивания, позволяющий корректно синтезировать алгоритмы, ориентированные на реализацию в реальном времени на транспьютерах, для широкого класса интеллектуальных динамических систем с внезапными возмущающими факторами. [22]
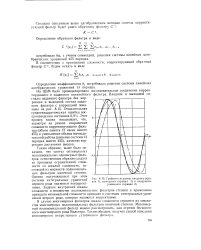 |
Графики сигналов. входного ( кри-ная /, выходного ( кривая 2 и скорректированного ( кривая 3. [23] |
Таким образом, выше было показано, что синтез оптимальных полиномиальных одномерных фильтров естественным образом следует из принципа ограниченной сложности со шкалой сложности, состоящей из множеств полиномиальных фильтров конечной степени. Однако получающиеся при этом системы интегральных уравнений первого рода являются некорректными. Задание внутренней шкалы сложности в множестве полиномиальных фильтров степени и применение принципа минимальной сложности приводят к системам интегральных уравнений второго рода, которые являются корректными. [24]
Во многих задачах теории оптимальных систем класс операторов, на котором находится решение задачи аналитического синтеза, настолько широк, что физическая реализация оптимального оператора, определенного в этом классе, представляет серьезные трудности или вообще является невозможной. Поэтому представляется целесообразным изменить постановку задачи аналитического синтеза. Пусть нам задан некоторый допустимый уровень качества р системы управления. Естественной является следующая постановка задачи аналитического синтеза. Среди всех операторов, обладающих допустимым уровнем качества, определить оператор, физическая реализация которого имеет минимальную сложность. Учитывая данное нами определение сложности, сформулируем принцип оптимальности оператора системы управления, который мы назовем принципом минимальной сложности. [25]
Страницы: 1 2