Судовой валопровод

Cтраница 2

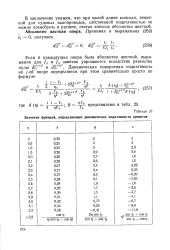Значения функций, определяющих динамические податливости пролетов. [16]

В заключение укажем, что при малой длине консоли, типичной для судовых валопроводов, собственной податливостью ее можно пренебречь в расчете, считая консоль абсолютно жесткой. [17]

Предлагаемый прием был применен при решении задачи оптимального проектирования резонансного преобразователя ( РП) для судовых валопроводов [4, 5], используемых в целях изменения ( снижения) уровня продольных колебаний механической системы, так как с его помощью можно воздействовать на собственные частоты системы сок. [18]

Схема валопровода. К. - Н - дейдвудное устройство. /. 2. 3 4 - опоры. [19]

Таким путем можно довольно быстро и с достаточной точностью определить интересующую нас первую собственную частоту судового валопровода со 1 / сек и далее N - 9 55со кол / мин. Эта частота должна быть отдалена от частот возбуждения на всем рабочем диапазоне, что обеспечивает работоспособность и надежность установки в отношении поперечных колебаний. [20]

Таким образом, в результате проведенного теоретического анализа получены основные формулы и соотношения, позволяющие представить судовой валопровод в виде многопролетной балки со ступенчатым изменением сечения и большой консольной массой и рассчитать частоты свободных поперечных колебаний такой системы. Эти соотношения заложены в основу излагаемой в следующем параграфе общей методики расчета поперечных колебаний судовых валопроводов. [21]

Таким образом, проведенный анализ показал, что допущения, обычно принимаемые при составлении расчетной схемы судовых валопроводов, недостаточно точно отражают свойства двух важнейших элементов реальной системы. Во-первых, особенности характеристик кормовой дейдвудной опоры не позволяют применить к ней общие рекомендации по замене реальной опоры точечной жесткой. Во-вторых, применяемая при составлении расчетной схемы замена гребного винта точечной массой на гибкой консоли также, по-видимому, не отвечает условиям действительности. Для правильного описания свойств дейдвудной опоры и гребного винта при расчете поперечных колебаний судовых валопроводов были поставлены и решены вспомогательные задачи, изложенные в следующем параграфе. [22]

Отпадает надобность в принудительном охлаждении, которое необходимо, например, в упорном и туннельных подшипниках скольжения судового валопровода. [23]

Кроме этого вида возбуждения, общего для всех систем, работа которых связана с вращением, возбудителями поперечных колебаний судовых валопроводов могут быть гидродинамические усилия на гребном винте. [24]

Общепринятая замена в расчете реальных опор точечными жесткими представляется вполне оправданной в применении к опорным подшипникам промежуточных валов, используемым в конструкциях судовых валопроводов. Эти подшипники имеют малую протяженность по сравнению с пролетами валопроводов. Поэтому, располагая точечную опору на середине длины подшипника, мы получаем достаточно хорошее представление системы в отношении изгибных жесткостей. [25]

Полученное уравнение представляет собой уравнение четвертой степени относительно fi2, корни его являются частотами свободных поперечных колебаний системы. В действительности судовые валопроводы имеют естественно не четыре, а бесчисленное множество частот свободных поперечных колебаний, так как сами податливости, играющие роль коэффициентов в полученном уравнении, определяются с учетом инерционных характеристик вала и зависят от частоты. [26]

Эти соотношения могут быть использованы для расчета консолей, а также пролетов с резким изменением сечения балки или с большими сосредоточенными массами. Последнее, вообще говоря, не характерно для судовых валопроводов; однако при установке винта регулируемого шага на одном из пролетов вала располагается большая масса ( механизм изменения шага), которая может быть заменена в расчете точечной сосредоточенной. [27]

Однако в многочисленных работах, посвященных проблеме поперечных колебаний судовых валопроводов, основное внимание уделяется не построению расчетной схемы, возможно более близкой по своим характеристикам к реальной системе, а разработке методов определения частот многопролетной балки постоянного сечения, лежащей на жестких точечных опорах, при наличии большой сосредоточенной массы на гибкой консоли. Как будет показано ниже, такое представление судового валопровода является лишь грубо приближенным, и результат расчета может поэтому существенно отличаться от истинной частоты свободных поперечных колебаний системы. Тем не менее рассмотрим вкратце основные методы решения задачи с использованием такой схемы, применяемые обычно на практике. [28]

В предыдущем параграфе при изложении существующих методов расчета поперечных колебаний судовых валопроводов были сформулированы основные допущения, принимаемые при составлении расчетной схемы. [29]

Страницы: 1 2 3