Проверка - согласие
Cтраница 1
Проверка согласия опытного и теоретического распределений была произведена для различных типов ТПР. [1]
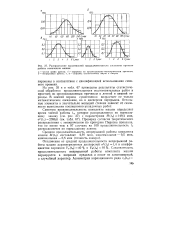 |
Распределение вероятностей продолжительности элементов времени-работы комплектов машин. [2] |
Проверка согласия теоретического распределения с эмпирическим по критерию Пирсона показала, что не менее чем в 97 случаях из 100 продолжительность / ч распределяется по нормальному закону. [3]
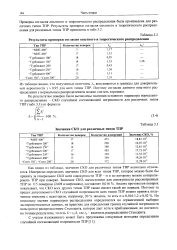 |
Результаты проверки согласия опытного и теоретического распределения. [4] |
Проверка согласия опытного и теоретического распределения была произведена для различных типов ТПР. [5]
Задача проверки согласия состоит в том, что по выборке из совокупности с генеральной функцией распределения G требуется проверить гипотезу о том, что G-F, где F - заданная непрерывная функция распределения. [6]
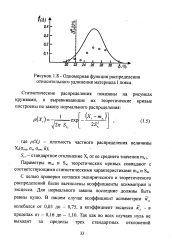 |
Одномерная функция распределения относительного удлинения материала I пояса. [7] |
С целью проверки согласия эмпирического и теоретического распределений были вычислены коэффициенты асимметрии и эксцесса. Для нормального закона последние должны быть равны нулю. [8]
При применении рекомендуемой методики проверки согласия для случая малых выборок установлены нижние пределы объемов выборочных данных, позволяющих с достаточной достоверностью определять основные характеристики генеральной совокупности случайной величины по выборочным данным малых объемов. [9]
Однако точность аппроксимации таким распределением мала, и проверка согласия по критерию Колмогорова отрицательная. Поэтому была сделана попытка заменить нормальное распределение распределениями Эрланга. [10]
СОГЛАСИЯ КРИТЕРИЙ - статистический критерии, применяемый в задаче проверки согласия, суп, к-рой заключается в следующем. [11]
С этой целью необходимо упорядочить содержащиеся в научной литературе результаты по проверке согласия опытного и теоретического распределения и издать документ, на основании которого следует решать указанные задачи. [12]
В связи с результатами случайных экспериментов довольно рано ставится вопрос о способах проверки согласия модели с экспериментом и о способах оценки неизвестных вероятностей по данным опыта. Эта тенденция возможно более раннего показа типичных статистических выводов, несомненно, целесообразна. [13]
Среди национальных стандартов по различным вопросам прикладной статистики имеются и стандарты по проверке согласия опытного и теоретического распределений. [14]
В SIAKRAPHICS реализованы метода дисперсионного анализа, кластерного анализа многомерного шкалирования и критерии проверки согласия для сложных гипотез. Широко представлены такие разделы статистики, как планирование эксперимента, логлинейный анализ, прогнозирование, использунцие в основном различные метода сглаживания. [15]
Страницы: 1 2 3