Проверка - точность - метод
Cтраница 1
Проверка точности метода была проведена на 25 искусственных смесях деароматизированных бензинов с 5 - 25 % ( по массе) аренов, взятых в соотношениях, воспроизводящих среднее распределение аренов в бензине. Далее, определив показатель преломления исходной фракции для желтой линии ( пд) с помощью номограммы [150], находят содержание циклоалканов и по. Таким образом, диеперсиомет-рический экспресс-метод определения группового состава заключается в измерении трех показателей преломления фрации ( п, п и п) без удаления аренов. [1]
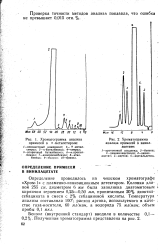 |
Хроматограмма анализа.| Хроматограмма анализа примесей в винил-ацетате. / - кротоновый альдегид. 2-бензол. [2] |
Проверка точности Методов анализа показала, что ошибка не превышает 0 015 отн. [3]
 |
Кривая зависимости U. [4] |
Проверка точности метода расчета цепи по участкам сводится к тому, что, взяв значение потока Ф0 120 9 - Ю-5 вб из опыта, определяют величины потоков Фе, Фет и Фт расчетным путем и сравнивают их с результатами опыта. [5]
Для проверки точности метода был приготовлен и проанализирован ряд синтетических смесей с различным содержанием бутиловых эфиров, а также технические образцы. [6]
Для проверки точности метода были составлены искусственные смеси с различным числом компонентов. Приготовление искусственных смесей углеводородов производилось в напускной системе ( см. рис. 1) путем дозировки каждого компонента из емкостей 5 в напускной баллон 1, предварительно эвакуированный до остаточного давления 10 - - 5 мм. [7]
Для проверки точности метода был проведен ряд анализов одной пробы. Эти данные представлены в таблице. [8]
Для проверки точности метода квазиодномерной схематизации была выбрана типичная двумерная задача совместной фильтрации несжимаемых жидкостей в горизонтальном пласте. Решение этой задачи было получено двумя методами: предлагаемым и традиционным конечно-р аз-ностным. Сравнение результатов обоих решений дает представление об эффективности квазйодномерной аппроксимации течения и соответствующего метода расчета. [9]
Для проверки точности метода диэлектрической криометрии проведен анализ ряда веществ с различными дипольными моментами и поляризуемостями. Метилнафталин, бензол и нафталин были выбраны как соединения со слабой поляризуемостью и небольшим дипольным моментом; я-дихлорбензол - как соединение, не имеющее дипольного момента, но легко поляризуемое; наконец, нитробензол - как типичное соединение с большим дипольным моментом. [10]
Для проверки точности метода квазиодномерной схематизации была выбрана типичная двумерная задача совместной фильтрации несжимаемых жидкостей в горизонтальном пласте. Решение этой задачи получено двумя методами: предлагаемым и традиционным конечно-разностным. Сравнение результатов обоих решений дает представление об эффективности квазиодномерной аппроксимации течения и соответствующего метода расчета. [11]
В целях проверки точности метода интегрирование системы дифференциальных уравнений стопорного режима осуществлялось и а ЭЦВМ Минск - 22М по стандартной программе методом Рунге - Кутта с автоматическим шагом и по программе, реализующей алгоритм II. [12]
С целью проверки точности метода параллельно проводилось определение f - числа вискозных растворов, полученных в аппарате ВА и по классическому способу. Вискозы различного способа приготовления подбирались таким образом, чтобы степень этерификации их была примерно одинакова. В таблице I для сопоставления приводятся данные определения гамма-числа и высоты волны для вискозных растворов, имеющих примерно одну и ту же степень отерификации, но различного способа приготовления. В последней графе таблицы дается отношение гамма-числа к вьтсоте волны. [13]
 |
Расчетная схема консольного стержня с сосредоточенной силой на конце. [14] |
С целью проверки точности метода рассчитывался прямой горизонтальный стержень шириной Ь 3 15 см, толщиной h 0 1 см и длиной L 51 8 см с жестко заделанным правым концом и загруженный на левом ( свободном) конце сосредоточенной вертикальной силой Р 5 25 Н ( рис. 3.11), которая в процессе деформации стержня остается вертикальной. Эта задача перемещения стержня под нагрузкой является плоской, геометрически нелинейной и имеет точное аналитическое решение, предложенное проф. [15]
Страницы: 1 2