Проверка - точность - метод
Cтраница 2
В целях проверки точности метода определения также полезно проводить контрольное определение. Для этого берут вещество, содержащее точно известное количество определяемого компонента, и производят его анализ таким же методом, каким производится анализ пробы неизвестного состава. [16]
В табл. 1 приведены результаты проверки точности метода на стандартных растворах железа, в табл. 2 - результаты определения содержания железа в образцах соляной кислоты различной степени чистоты. [17]
Для ряда особых случаев известны аналитические решения ( Маскет, 1937; Коллинз, 1961), которые попутно можно использовать для проверки точности методов аппроксимации. Помимо этого, большая часть понятий, относящихся к конечно-разностным методам, и методика численного решения представлены здесь в доступном виде и могут быть в дальнейшем распространены для многомерной фильтрации. В данной книге понятие размерность относится только к пространству, но не ко времени, поэтому нестационарная задача в координатах х и t одномерна. [18]
Большой интерес представляет расчет кривой ММР из кинетических данных и сравнение ее с экспериментально полученной кривой. Это важно и для уточнения кинетической схемы, и для проверки точности метода измерения ММР при известной схеме. [19]
В этом случае алгебраические выкладки более громоздки, но все еще осуществимы. Следует заметить, что полученные значения пХ2 мало отличаются от предыдущих; это еще одна проверка точности метода. [20]
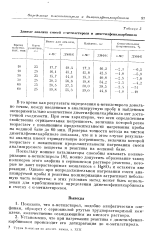 |
Данные анализа смесей а-метилстирола и диметилфенилкарбпнола. [21] |
В то время как результаты определения а-метилстирола довольно точны, между введенным в анализируемую пробу и найденным экспериментально количеством диметилфенилкарбинола нет достаточной сходимости. При этом характерно, что всем определениям свойственна отрицательная погрешность, величина которой резко возрастает с повышением продолжительности нагревания пробы на водяной бане до 60 мин. Проверка точности метода на чистом диметилфенилкарбиноле показала, что и в этом случае результаты анализа имеют отрицательную погрешность, величина которой возрастает с повышением продолжительности нагревания смеси анализируемого вещества и реактива на водяной бане. [22]
При изготовлении стандартов применялась очищенная от гафния окись циркония и 92-процентный препарат гафния. Для проверки точности метода проводился подсчет абсолютного количества гафния в 17 синтетических пробах, изготовленных из трех исходных проб, причем количество гафния в исходных и конечных пробах определялось спектроскопически. Баланс сошелся в пределах ошибки, равной - 1 5 %, что свидетельствует о хорошей точности метода. [23]
Касаясь иода, он констатировал, что найденная им плотность ( d 8 716) соответствует атомному весу иода, равному 790 4 ( О 100), что достаточно близко к величине, которую косвенным путем нашел Гей-Люссак; этот атомный вес также соответствует плотности йодистого водорода, найденного Гей-Люссаком ( с. Объясняя цель данного определения плотности паров иода, Дюма писал: Я хотел это сделать по многим соображениям: во-первых, для замены гипотезы ( правда, весьма вероятной) положительными опытными данными; во-вторых, для проверки точности метода, которым я пользовался [ 47, стр. [24]
Квадраты коэффициентов этой линейной комбинации равны плотности неспаренногб электрона. Если 2ре - 1, то по известной спиновой плотности предварительно находят электронную плотность. Полученная молекулярная орбиталь может быть применена для проверки точности приближенных квантово-химических методов расчета, а также для расчета различных констант радикала. [25]
Возмущением является слабая нелинейность восстанавливающей силы, обусловленной наличием пружины. При а О имеют место свободные колебания с частотой со ] / / т, не зависящей от амплитуды движения. Из физических соображений ясно, что вследствие зависимости упругой силы пружины от амплитуды период также должен зависеть от амплитуды, а при а О ( мягкая пружина) движения с большой амплитудой неограниченны. Следует заметить, что уравнение (3.1.2) является некоторой аппроксимацией ( а 0) уравнения движения простого маятника. Точное решение уравнения (3.1.2) может быть также выражено через эллиптические интегралы и использовано для проверки точности метода возмущений, развитого здесь. [26]
Страницы: 1 2