Выпуклое программирование

Cтраница 2

Существенной особенностью задач выпуклого программирования является совпадение точек локального и глобального экстремумов. Это означает, что при решении задач выпуклого программирования можно довольствоваться отысканием локального экстремума. [16]

Пусть решение задачи выпуклого программирования ( 4), ( 5) существует и достигается в точке х, не обязательно единственной. Тогда для того чтобы задача ( 4), ( 5) была эквивалентна задаче отыскания безусловного минимума функции ( 9) при а, большем некоторого а, необходимо и достаточно, чтобы смешанная система неравенств ( 10) была несовместна. [17]

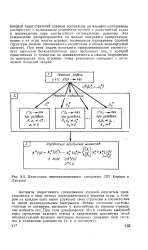Блок-схема декомпозиционного алгоритма ЛП Корнай и Липтака. [18]

При этом задаче выпуклого программирования соответствует выпуклая бескоалиционная игра нескольких лиц, у которой единственная ( с точностью до эквивалентности в смысле безразличия по выигрышам всех игроков) точка равновесия совпадает с опги - MVMOM исходной задачи. [19]

В настоящее время задачи выпуклого программирования хорошо изучены. [20]

В настоящее время теория выпуклого программирования уже разработана. Общие же методы решения задач нелинейного невыпуклого программирования отсутствуют. [21]

Важное место в теории выпуклого программирования занимают условия Куна-Таккера, названные так в честь открывших их американских математиков Куна и Таккера. [22]

КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ - раздел выпуклого программирования, при котором целевая функция представляет собой многочлен второй степени, а ограничения линейны. [23]

Рассматривается возможность сведения задачи выпуклого программирования к задаче отыскания экстремума негладкой штрафной функции. [24]

КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ - раздел выпуклого программирования, посвященный теории и методам решения задач минимизации выпуклых квадратичных функций на множествах, задаваемых системами линейных неравенств и равенств. Существует законченная теория К. [25]

Таким образом, задача выпуклого программирования сводится к решению системы уравнений и неравенств. На основе теоремы Куна - Такера разработаны различные итерационные методы минимизации, сводящиеся к поиску седловой точки функции Лагранжа. [26]

Теорема 2.5. В задачах выпуклого программирования относительный минимум является абсолютным минимумом. [27]

Однако рассматриваемый нами случай строго выпуклого программирования в этом отношении вполне благополучен: функция R ( g) дифференцируема. Более того, ее производная dR / dg вычисляется достаточно просто, и нет необходимости прибегать к численному дифференцированию. [28]

К регулярным относятся задачи линейного и выпуклого программирования. К нерегулярным, наряду с дискретными, относятся многоэкстремальные задачи, в которых локальный экстремум может не совпадать с глобальным. Дискретные задачи характеризуются тем, что область допустимых решений невыпукла и несвязна, а это делает невозможным решение их с помощью стандартных методов, применяемых для решения регулярных задач математического программирования. [29]

Двухэтапные задачи сводятся к выпуклому программированию и решаются методами выпуклого программирования. К двухэтапным задачам сводятся многие задачи теории управления запасами. [30]

Страницы: 1 2 3 4