Производная - сумма
Cтраница 3
При последовательном соединении нескольких нелинейных элементов дифференциальное сопротивление результирующей характеристики при каком-то токе равно сумме дифференциальных сопротивлений нелинейных элементов при этом же токе. Это правило основано на том, что производная суммы равна сумме производных. [31]
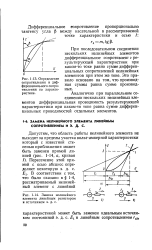 |
Определение сопротивления и дифференциального сопротивления по характеристике.| Замена нелинейного элемента линейным резистором и источником э. д. с. [32] |
При последовательном соединении нескольких нелинейных элементов дифференциальное сопротивленг г результирующей характеристики при каком-то токе равно сумме дифференциальных сопротивлений нелинейных элементов при этом же токе. Это правило основано на том, что - производная суммы равна сумме производных. [33]
Так как ускорение - это производная скорости по времени, то для того, чтобы найти его значение, нужно продифференцировать эту формулу. Вспомним теперь одно из правил табл. 8.3, а именно что производная суммы равна сумме производных. [34]
Постановка задачи нам теперь уже ясна. Сумма конечного числа функций, дифференцируемых в некоторой точке х, также дифференцируема в этой точке, и производная суммы равна сумме производных слагаемых. Мы хотим знать, при каких условиях это правило может быть перенесено на бесконечные ряды функций. [35]
Страницы: 1 2 3