Сложный процент
Cтраница 3
Полугодовое начисление сложных процентов обычно используется при определении доходности к погашению для облигаций, так как купонные выплаты, как правило, делаются дважды в год. [31]
При использовании сложных процентов сумма дохода на вложенные средства исчисляется из суммы первоначального взноса плюс начисленные проценты, т.е. с наращенной суммы. [32]
Если ставка непрерывно начисляемого сложного процента равна 10 % в год, 1 дол. [33]
Наращение по сложным процентам описывается геометрической прогрессией. [34]
Наращение по сложным процентам относится к периодическому добавлению накопленных процентов к основной сумме долга, т.е. накопленные проценты добавляются к основной сумме, увеличивая тем самым ее размер. Проценты в дальнейшем начисляются уже на эту увеличенную сумму. Например, денежная сумма в размере 1000 единиц помещается на банковский депозит на срок 3 года с годовой процентной ставкой 6 % и ежегодным начислением процентов. [35]
Наращение по сложным процентам относится к периодическому добавлению накопленных процентов к основной сумме долга, то есть накопленные проценты добавляются к основной сумме и полученная увеличенная сумма является исходной для начисления процентов в следующем периоде. При фиксированной процентной ставке инвестирование на один период, соответствующий процентной ставке по сложным и простым процентам, приводит к одному и тому же наращенному значению. Поэтому начисление сложных процентов эквивалентно начислению простых процентов при реинвестировании средств в конце каждого периода. [36]
Наращение по сложным процентам описывается геометрической прогрессией. [37]
Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности. [38]
Применение формулы (5.1) сложных процентов для учета фактора времени до недавнего времени считалось некоторыми экономистами неправомерным, так как эта формула якобы противоречит природе процесса образования стоимости и будто бы допускает самовозрастание капиталовложений во времени. При этом ссылаются на критику К. [39]
Применение формулы (5.1) сложных процентов предполагает, что вся величина ежегодного эффекта от временно высвобожденных капиталовложений К обращается на производственное накопление. На создание производственных фондов ежегодно используется не весь эффект, а только часть его, доля которой может быть принята равной доле v производственных капиталовложений в национальном доходе. [40]
Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности. [41]
Принцип непрерывного начисления сложного процента имеет особое значение при планировании долгосрочных вложений, когда более обоснованно считать, что поток денежных средств поступает равномерно в течение года, а не в конце года. [42]
Расчеты по правилу сложных процентов часто называют НАЧИСЛЕНИЕМ ПРОЦЕНТОВ НА ПРОЦЕНТЫ, а процедуру присоединения начисленных процентов - их РЕИНВЕСТИРОВАНИЕМ, или КАПИТАЛИЗАЦИЕЙ. [43]
Использование в расчетах сложных процентов более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. Считается, что по мере получения любых денежных поступлений, в силу требования рациональности, последние должны наращиваться либо в ходе данного инвестиционного проекта, либо в других инвестиционных проектах. [44]
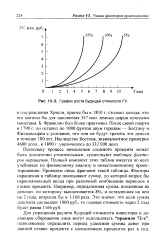 |
График роста будущей стоимости FV. [45] |
Страницы: 1 2 3 4