Случайный процесс - нагружение
Cтраница 3
Характер и величина нагрузки и от испытания к испытанию не меняются. Вследствие стационарности случайного процесса нагружения и ( t) наибольшие случайные значения его на интервалах, равных ткор, подчиняются одному и тому же закону распределения. [31]
Если процесс нагружения состоит из циклов с часто и в большом диапазоне меняющимися уровнями амплитуд напряжений, использование соотношения (5.23) для оценки эффекта торможения трещин становится затруднительным. Особенно интересны в этом отношении случайные процессы нагружения. В этих и подобных случаях необходимо учитывать всю историю нагружения. Однако если случайные процессы заданы, например, в виде корреляционных функций или энергетических спектров, то такая информация отсутствует. Поэтому интересен такой способ учета эффекта торможения трещин, в котором принимается во внимание изменение скорости роста трещин только для таких циклов, которым предшествуют циклы с большими значениями амплитуд напряжений и эффект торможения ограничивается первым следующим циклом нагружения. [32]
При детерминистическом нагружении эга связь задана формулой (3.105), согласно которой математическое ожидание числа зародышей, а также развившихся из них трещин есть функция от меры повреждений г)) ( t) в рассматриваемый момент времени. Обобщим эту гипотезу применительно к случайным процессам нагружения. Примем, что образование зародышевых трещин представляет собой пуассоновский процесс. Этот процесс определен, если задана его интенсивность, равная числу трещин, зарождающихся в единицу времени. Обсудим два, в общем случае не совпадающих, способа обобщения формулы (3.105) на случайные условия нагружения. [33]
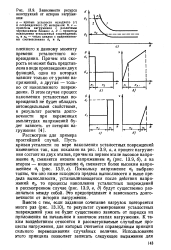 |
Зависимости ресурса конструкций от истории нагружения. [34] |
Вместе с тем, если заданное сочетание нагрузок повторяется много раз ( рис. 13.10), то результат суммирования усталостных повреждений уже не будет существенно зависеть от порядка их приложения на начальном и конечном этапах нагружения. К таким воздействиям относятся и рассматриваемые случайные процессы нагружения, для которых считается справедливым принцип сильного перемешивания случайных величин. [35]
Осреднение влияния последовательности приложения нагрузок наступает при сравнительно больших емкостях блока, поэтому естественно предположить, что уменьшение числа циклов в пределах каждого уровня напряжений и переход в конечном счете к однократному нагружению в любой последовательности ( при случайном чередовании нагрузок) не изменят результатов испытаний. Так, основываясь на экспериментальных данных, можно показать, что при исследовании закономерностей накопления усталостного повреждения воспроизведение случайного процесса нагружения может быть заменено регулярной схематизированной программой дискретного типа. [36]
Описанные характеристики сопротивления металлов усталости относятся к случаю относительно большого числа циклов нагружения и малых уровней напряжений по сравнению со значением предела прочности. Охват всего диапазона возможных значений действующих напряжений требует дополнительной экспериментальной информации, а необходимость решения этой задачи обусловлена тем, что в случайных процессах нагружения ( которые рассматриваются в данной работе) не исключается появление редких, но больших значений напряжений, превышающих предел текучести и предел прочности материала конструкции. Для учета этого обстоятельства заметим, что уравнение кривой усталости ( 1 2) при напряжениях, превышающих предел прочности, теряет смысл, а при напряжениях, превышающих предел текучести, требует уточнения, так как в этом случае изменяется сам механизм разрушения: из области многоцикловой усталости он переходит в область малоцикловой усталости. [37]
Статистические характеристики эксплуатационной нагруженности, необходимые для расчета на выносливость, получаются на основе обработки результатов тензометрирования. Рядом организаций ( НАТИ, ИМАП1 АН СССР, ВНИИНМАШ, ИМЕХ АН УССР, МАИ, ЗИЛ, ВИСХОМ) разработан ГОСТ 25.101 - 83, согласованный со стандартом ГДР, в котором изложены методы схематизации случайных процессов нагружения элементов машин и статистического представления результатов. Использование данных методов позволяет получить необходимую для расчетов статистическую информацию о нагруженности. [38]
Достоверность расчета живучести можно значительно повысить, если учесть еще эффект торможения трещин, наблюдаемый при смене уровней напряжений в соседних циклах процесса нагружения. В случайных процессах нагружения такая смена уровней напряжений происходит постоянно, и поэтому эффект торможения трещин может быть значительным. [39]
Однако в большинстве автомобильных деталей переменные напряжения возникают не вследствие вращения деталей, а в результате изменения внешних нагрузок Q. Для оценки усталостной долговечности таких деталей необходимо знать амплитуды переменных нагрузок. Распределение амплитуд непрерывного случайного процесса нагружения может быть получено несколькими способами статистической обработки. Однако необходимо учитывать, что разные способы систематизации процесса дают спектры, различные по интенсивности повреждающего воздействия. [40]
Рассмотрим нагружение, при котором известна плотность вероятности амплитуды переменного напряжения, показывающая насколько часто появляются переменные напряжения заданной величины. На рис. 6.11 приведена плотность распределения переменных напряжений в лопатках компрессора. Предполагаем, что случайный процесс нагружения обладает свойством эргодичности. [41]
Решающую роль в расчете на усталостную долговечность играет информация о нагруженно-сти тех или иных зон конструкции, которые, как было показано выше, могут иметь широкий спектр видов напряженного состояния. Реально действующие на ВС нагрузки используют в расчете долговечности элементов конструкций после соответствующей модификации их спектра путем представления его как регулярного. Экспериментальные исследования нагруженности предполагают представление изучаемых случайных процессов нагружения схематично в результате различной систематизации внешних нагрузок. Схематизация нагрузок подразумевает введение некоторого алгоритма, позволяющего заменить исходный процесс нагружения таким процессом, который должен быть ему эквивалентен по величине повреждающего воздействия. Процессы считаются эквивалентными, если функции распределения усталостной долговечности конструктивного элемента при воздействии этими процессами совпадают. [42]
При отработке конструкций проводят анализ зависимости параметров от нагрузок. Для этого в определенных точках конструкции устанавливают необходимое количество датчиков ( с требуемыми диапазоном и точностью измерений), которые непрерывно регистрируют процессы, связанные с изменением нагрузки. При этом ни вид корреляционной функции, ни другие характеристики случайного процесса нагружения не известны. [43]
Таким образом, в рамках данной теории разброс долговечности при детерминистическом нагружении целиком возникает на инкубационной стадии, в то время как продолжительность стадии роста трещины является величиной детерминистической. В статьях [11, 14] объединенная теория разрушения распространена на неоднородные ( но медленно изменяющиеся) поля напряжений и механических свойств материала, а также на случайные процессы нагружения. [44]
Следует указать, что при случайном нагружении понятия цикла, еднего значения и амплитуды носят условный характер в отличие г гармонического процесса. Фактически речь идет о полусуммах и луразностях соседних максимумов и минимумов. Поскольку, ис -) льзуемое в формуле (2.8) уравнение кривой усталости соответствует: пытаниям с гармоническими циклами, возникает проблема такой фаботки ( схематизации) случайного процесса нагружения, чтобы [ ематизированньш процесс был эквивалентен исходному по степени эвреждающего воздействия. [45]
Страницы: 1 2 3 4