Мультипликативный процесс

Cтраница 1

Мультипликативный процесс порождает популяцию, которая концентрирует подавляющую часть первоначально равномерно распределенной популяции на множестве-носителе. [1]

Вейвлет-анализ предоставляет визуальные свидетельства существования мультипликативного процесса, лежащего в основе временного порядка следования событий. [2]

Популяции или распределения, порождаемые мультипликативным процессом, находят многочисленные применения и обладают тем преимуществом, что многие свойства таких распределений легко поддаются анализу. [3]

Эти уравнения совпадают с уравнениями (6.7), описывающими меру мультипликативного процесса, который обсуждался в разд. Эта вероятность ( мера) является растущей функцией х, причем эта функция сингулярна в том смысле, что почти всюду ее наклон равен нулю. Длина кривой М ( х) равна L 2, поэтому это не фрактальная кривая, а фрактальная мера ( см. обсуждения в разд. [4]

Мы полагаем, что наиболее адекватное описание процессов на выходе ФРНУ можно получить, используя модель нестационарных мультипликативных процессов. При этом нестационарные аддитивные процессы на выходе ФРНУ, иботающего в режиме фоновой активности, можно рассматривать как частный случай функционирования мультипликативном стохастической системы регулирования, когда связь между основным и дополнительными контурами отсутствует. [5]

Мультифрактальный спектр для одномерных сечений, проведенных через диссипационное поле в полностью развитых турбулентных течениях ( турбулентность за решеткой, след за круговым цилиндром, пограничный слой, атмосферная турбулентность. Квадратики соответствуют экспериментальным средним, сплошная кривая / ( а - биномиальному мультипликативному процессу с р 0 7. [6]

В работе Менево и Сринивасана [160] показано, что экспериментальные данные по полностью развитой турбулентности очень хорошо описываются только что представленным мультипликативным процессом. [7]

Это и есть уравнение для функции т ( д), а функция Ti ( q r) называется генератором для такого мультипликативного процесса разбиения множества. [8]

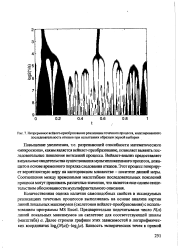Непрерывное вейвлет-преобразование реализации точечного процесса, моделировавшего последовательность отказов при испытаниях образцов первой выборки. [9]

Повышение увеличения, т.е. разрешающей способности математического микроскопа, каким является вейвлет-преобразование, позволяет выявить последовательные поколения ветвлений процесса. Вейвлет-анализ предоставляет визуальные свидетельства существования мультипликативного процесса, лежащего в основе временного порядка следования отказов. Этот процесс генерирует вероятностную меру на канторовском множестве - носителе данной меры. [10]

N ( Qi близка к своему максимуму. Эти множества имеют фрактальную размерность, определяемую энтропией мультипликативного процесса. Разумеется, аналогичные рассуждения приводят к заключению о том, что конечная доля точек отрезка содержится в множествах с Ь, к 1 / 2, для которых величина N ( Q близка к своему максимуму. [11]

Вейвлет-анализ эмпирических данных о последовательности событий позволяет выявить ее мультифрактальную природу. Использование непрерывного вейвлет-преобразования является эффективным инструментом для обработки и анализа данных и обеспечивает визуальные свидетельства существования мультипликативного процесса, лежащего в основе временной структуры последовательности событий. Этот процесс генерирует вероятностную меру на канторовском множестве - носителе данной меры. [12]

Показатель не очень удобен, и на практике предпочитают пользоваться показателем Липшица-Гельдера а ( см., например, [ 134, с. Особенности меры М ( х) характеризуются показателем а. Рассмотрим меру, порожденную мультипликативным процессом в и-м поколении. [13]

Вейвлет-анализ обеспечивает двухмерную развертку одномерного сигнала, при которой и время, и масштаб ( частота) рассматриваются как независимые переменные, что позволяет анализировать временной ряд одновременно во временной и в частотной областях. Вейвлет-преобразование помогает визуализировать самоподобные или самоаффинные свойства фрактальных объектов, хорошо приспособлено к анализу каскадных процессов, моно-и мультифрактальных множеств и вероятностных мер, имеющих иерархическую природу. В частности, оно наглядно выявляет иерархический мультипликативный процесс, генерирующий вероятностную меру и управляющий относительным расположением событий на оси времени. Мультимасш-табные структуры, выявляемые в последовательности событий, являются темпоральными структурами, развернутыми в относительно широком диапазоне масштабов реального времени, в отличие от фрактальных аттракторов, которые существуют в фазовом пространстве. Поэтому вейвлет-преобразо-ванию могут быть подвергнуты непосредственно реализации точечного процесса, полученные путем статистического моделирования последовательности событий, при испытаниях или в реальных условиях. [14]

Кроме того, он оставит у себя некоторое количество, предположим 5 ден. Если принять во внимание, что во всех последующих расчетах из мультипликативного процесса вычитаются не только доля, сохраняемая как обязательный резерв ( гг), но и доля, хранимая банками как собственный резерв, и та, которую накопит ( оставит на руках) население, то в результате само расширение депозита окажется меньше, чем в предыдущих наших расчетах. [15]

Страницы: 1