Квазистационарный процесс
Cтраница 2
Диффузия в пленке рассматривается как квазистационарный процесс. [16]
 |
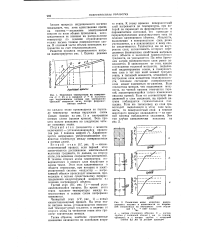
Типичный вид зависимости q. [17] |
Рассматривая течение в скважине как квазистационарный процесс, допустим, что зависимости, получаемые в опытах по стационарному течению, применимы и для описания исследуемого здесь явления. [18]
Рассматривая процесс горения капли как квазистационарный процесс диффузии и теплообмена, можно рассчитать время горения капли и ее температуру в период испарения. [19]
Напомним, что обязательным признаком квазистационарного процесса является наличие лимитирующей стадии. С учетом этого для описания кинетики реакции достаточно рассмотреть случаи различных лимитирующих стадий. [20]
Из общих уравнений Максвелла для квазистационарных процессов нетрудно получить основные уравнения для токов в системе квазилинейных проводников, обычно используемые при расчете линейных цепей, содержащих такие элементы, как резисторы, конден саторы и катушки индуктивности. [21]
Из общих уравнений Максвелла для квазистационарных процессов нетрудно получить основные уравнения для токов в системе квазилинейных проводников, обычно используемые при расчете линейных цепей, содержащих такие элементы, как резисторы, конденсаторы и катушки индуктивности. [22]
Решение многих статистических задач для квазистационарных процессов часто сводится к стационарному случаю. [23]
В настоящем параграфе мы рассмотрим особый случай квазистационарных процессов - токи высокой частоты, для которых остаются справедливыми условия (8.1), (8.2), но теряется понятие электрической цепи как совокупности элементов с сосредоточенными параметрами. Тем самым будут получены дополнительные к (8.1), (8.2) условия того, что систему проводников можно будет рассматривать как электрическую цепь. [24]
Такое поле скоростей можно использовать дня моделирования многих стационарных и квазистационарных процессов ОМД, в которых в качестве модели металла допустимо применение сплошной несжимаемой среды. В некоторых частных случаях, имеющих большое прикладное значение, вид поля (1.2.121) существенно упрощается. Нижеследующая серия упражнений посвящена таким случаям. [25]
Ее моищо упростить, если рассматривать внешнюю диффузию как квазистационарный процесс. [26]
Как было показано в предыдущих главах, детальное моделирование квазистационарных процессов распространения в пламенах предварительно перемешанной смеси и предварительно не перемешанной смеси с учетом молекулярного переноса, химических реакций, термодинамики и конвекции является очень трудной проблемой, которая почти всегда требует численного решения. Поэтому не удивительно, что переход к нестационарной ( зависящей от времени) задаче воспламенения еще более требователен к возможностям численного моделирования таких процессов на ЭВМ. [27]
Данный пример иллюстрирует метод, основанный на представлениях о квазистационарных процессах. Сущность метода заключается в том, что используются уравнения, обоснованные для стационарных процессов ( гидродинамических и массообменных), для оценки массообмена в нестационарных условиях. Правомерность такого подхода сомнительна, в особенности при больших ускорениях потока жидкости. И все же он применяется ввиду его относительной простоты. Вращательное движение жидкости также создает условия для нестационарного массообмена. [28]
В закрытых системах стационарные процессы невозможны, однако, осуществимы квазистационарные процессы. Положим, что реакция проходит последовательно через ряд элементарных актов, каждый из которых обладает собственной скоростью. [29]
Страницы: 1 2 3 4