Квазистационарный процесс

Cтраница 3

Второй этап ( / /, рис. 1) - квазистационарный процесс; если первый этап заканчивается достижением максимальной величины градиента, то дальше, на втором этапе, эта величина сохраняется неизменной. В течение второго этапа температура поверхностного и осевого слоя возрастает в одном темпе. Этот этап заканчивается в области температур, при которых в электромагнитной системе индуктор - нагреваемый объект происходят изменения, приводящие к весьма существенному перераспределению индуктируемой мощности по сечению нагреваемого объекта. [31]

Таким образом, теплообмен в верхней части слитка можно считать квазистационарным процессом с осевым градиентом температуры по вертикали. Для анализа такого процесса нужно знать форму лунки жидкого металла или зависимость площади поверхности лунки от ее периметра, что можно получить расчетом процесса кристаллизации металла в лунке. [32]

Какую роль играют начальные условия при решении дифференциальных уравнений, описывающих квазистационарные процессы в цепях, содержащих конденсаторы или индуктивности. [33]

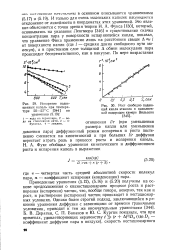
Результаты расчета температур в период теплонасыщения. [34]

Из сопоставления кривых на рис. IV.26 следует, что если при квазистационарном процессе металл в точках у 1 см при рассматриваемом режиме нагрева получает температуру более 1500 С и расплавляется, то в начальном участке выполняемой наплавки максимальная температура точки у 1 см достигает только - 1160 С. [35]

Таким образом, при прохождении переменного тока в плазме столба дуги происходит квазистационарный процесс, заключающийся в том, что при изменении напряженности поля и тока периодически изменяются число заряженных частиц и проводимость дугового промежутка. Высокая температура среды и электродов способствуют сохранению условий, практически обеспечивающих эмиссию с катода при переходе напряжения через нуль и восстановления проводимости промежутка со скоростью изменения напряжения. Именно поэтому кривая тока здесь не имеет заметных разрывов и при перемене знака плавно проходит через нуль. По этим же причинам динамическая вольт-амперная характеристика рассматриваемой дуги представляет собой прямую линию ( рис. 5 - 6) как для мгновенных, так и для максимальных значений напряжения и тока. [36]

Классическая теория постоянного или выпрямленного электрического тока в электролитах основана на предположении квазистационарных процессов. Рассматривая такую систему, отметим, что между электродамп и электролитом происходит обмен энергии, имеет место переход матери. Поскольку во всяком потоке электромагнитного излучения заключается не только определенная энергия, но и определенный импульс, всегда совпадающий с направлением излучения, то, следовательно, квант энергии заключает в себе определенный квант импульса, который и сообщает материальной частице толчок, совершая таким образом работу выхода материальной частицы. При переходе заряженной частицы с поверхности электрода в электролит происходит потеря ( отражение) энергии, зависящая от диэлектрических и магнитных свойств среды, под влиянием которых существует та или иная контактная разность потенциалов электрод-электролит. С точки зрения волновой теории отражение происходит без изменения длины волны. Исходя же из квантовой теории длина волны может изменяться, если изменится размер кванта энергии. [37]

Базовая система уравнений ( 1) - ( 8) справедлива для квазистационарных процессов адиабатического течения газа в дросселях и изотермического изменения параметров его состояния в камерах. [38]

Испарение подвешенных капель при температуре 20 - 22 С по уравнению.| Рост свободно падающей капли этанола в наполненной водородом камере Вильсона. [39]

Приведенные уравнения (5.12), (5.16) и (5.20) получены на основе предположения о квазистационарном процессе роста и растворения ( испарения) частиц, что, вообще говоря, неверно, так как и рост, и растворение ( испарение) частиц происходят в нестационарных условиях. [40]

Асимптотический режим необратимой диссоциации, рассмотренный в § 1, является частным случаем квазистационарного процесса. [41]

Обычно для расчета коэффициента скорости растворения используют метод, основанный на представлении о квазистационарном процессе. Сущность метода состоит в том, что применяют уравнения, обоснованные для стационарных процессов, для оценки кинетики растворения в нестационарных условиях. Если коэффициент К изменяется от минимального до максимального значения, то выполняют осреднение за период, в течение которого происходит это изменение. Этот коэффициент и является характеристикой кинетики. [42]

Расчет последовательности ( V, 46) производится для стационарных случайных процессов или для квазистационарных процессов, полученных в результате центрирования. Если центрирование осуществляется путем фильтрации, то сходимость последовательности ( V, 46) зависит от характеристик фильтра, использованного при центрировании. Правильность выбора фильтра, а следовательно и значения Т, может быть проверена только после расчета спектральной плотности случайного процесса. [43]

АЭ меняются со временем сравнительно медленно, что дает возможность описывать данный вид эмиссии как квазистационарный процесс. [44]

Мы убедились в том, что гиббсовское определение равновесной энтропии приводит к термодинамическим соотношениям, определяющим изменение энтропии в квазистационарных процессах. Напомним, однако, что в феноменологической термодинамике определяется и абсолютное значение энтропии как следствие из третьего закона термодинамики, или теоремы Нернста. Покажем, как теорема Нернста может быть обоснована в рамках метода статистических ансамблей. [45]

Страницы: 1 2 3 4