Сложный колебательный процесс
Cтраница 2
Первая из этих характеристик показывает, как изменяются параметры сложного колебательного процесса во времени; вторая устанавливает, как распределяются величины этих параметров в-любой момент времени по частотам слагаемых колебаний. Гра - - фическое изображение амплитудно-временной характеристики вибрационного процесса обычно называют осциллограммой или виброграммой процесса, а амплитудно-частотной характеристики - его спектрограммой. [16]
На рис. 6 видно, что полученная амплитудно-временная характеристика сложного колебательного процесса не является синусоидой, а следовательно, сложный колебательный процесс не является гармоническим. Кроме того, можно указать, что форма колебаний для отдельных его параметров х, v, а, из-за множителя со для скорости и со2 для ускорения также не сохраняется. [17]
Обратим внимание на то, что частота повторения формы сложного колебательного процесса, как это следует из равенства ( 2 - 2 - 4), может не совпадать ни с одной из частот слагаемых колебаний. [18]
После окончания действия питающего импульсного напряжения в трансформаторной цепи возникает сложный колебательный процесс. Этот процесс при наличии в трансформаторной цепи элементов, обладающих вентильными свойствами, может быть весьма интенсивным и нарушить нормальную работу всего импульсного устройства. Сложность колебательного процесса связана с тем, что во всех реактивных элементах трансформаторной цепи в момент окончания действия импульса запасена электрическая и магнитная энергия. Так как число таких элементов велико, то колебательный процесс описывается решением дифференциального уравнения высокого порядка. [19]
Равенство показывает, что и в этом случае в бруске возникает сложный колебательный процесс, образуемый наложением синусоидальных колебаний, возбуждаемых на всех частотах собственных продольных колебаний стержня. [20]
Таким образом, введение понятия эквивалентного притока позволило свести задачу построения сложного колебательного процесса к линейному дифференциальному уравнению (9.10), которое хорошо изучено. [21]
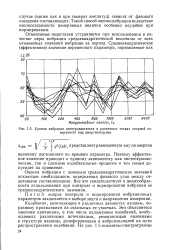 |
Уровни вибрации электродвигателя в различных точках опорной поверхности над амортизаторами. [22] |
Поэтому эффективное значение приводит к единому эквиваленту как чистогармони-ческие, так и сложные колебательные процессы и тем самым допускает их сравнение. [23]
Как уже было указано, при неравномерном движении тяговой цепи в последней возникает сложный колебательный процесс, сочетающий в себе как вынужденные колебания от периодически изменяющихся внешних динамических нагрузок, так и свободные колебания упругой цепи. Максимально возможные нагрузки возникнут при резонансе, когда периоды свободных и вынужденных колебаний цепи будут одинаковы. Обобщенным коэффициентом динамичности Кд можно приближенно учесть, насколько близко действующие нагрузки соответствуют максимально возможному случаю. [24]
 |
Предельно допустимые амплитуды вибрации центробежных компрессоров. [25] |
Эффективное значение скорости вибрации позволяет оценивать и сравнивать между собой как простые ( гармонические), так и сложные колебательные процессы. Значение эффективной скорости вибрации может быть измерено приборами либо рассчитано на основе анализа спектра частот вибрации. [26]
На рис. 6 видно, что полученная амплитудно-временная характеристика сложного колебательного процесса не является синусоидой, а следовательно, сложный колебательный процесс не является гармоническим. Кроме того, можно указать, что форма колебаний для отдельных его параметров х, v, а, из-за множителя со для скорости и со2 для ускорения также не сохраняется. [27]
В анализаторах колебаний и анализаторах спектра случайных процессов признаком разделения является частота колебаний ( длины волны), а признаком измерения - амплитуда или средняя мощность каждой гармонической составляющей сложного колебательного процесса. [28]
Из-за несовершенной магнитной связи между обмотками импульсного трансформатора, наличия емкостных связей обмоток и других реактивных элементов в питающей и нагрузочной цепях трансформатора, при воздействии на трансформатор импульсов напряжения, с крутым фронтом, а также после окончания импульса, в трансформаторной цепи возникает сложный колебательный процесс. Этот колебательный процесс оказывает существенное влияние на работу импульсного трансформатора, обусловливая искажения формы трансформируемых импульсов. Это обстоятельство определяет основные особенности импульсных транформаторов, требуя максимального уменьшения паразитных параметров трансформаторной цепи. Поэтому большое значение приобретает вопрос аналитического и экспериментального исследования колебательных процессов в трансформаторной цепи. [29]
В предыдущей главе было показано, что возмущение стержня распространяется вдоль его длины в форме волны, которая отражается на конце стержня. Возникает сложный колебательный процесс, причем он должен был бы продолжаться бесконечно долго. Однако из опыта известно, что это явление достаточно быстро затухает и что крутизна фронта волны постепенно снижается. Поэтому необходимо вывести новое уравнение движения с учетом возможного затухания. [30]
Страницы: 1 2 3 4