Авторегрессионный процесс

Cтраница 1

Авторегрессионные процессы принято выражать в терминах оператора сдвига назад В. [1]

Авторегрессионный процесс и процесс скользящей средней, который мы проанализируем в следующем параграфе, предполагают, что анализируемые данные являются стационарными. [2]

R / S - анализ стохастических процессов. [3]

Авторегрессионный процесс - это процесс, в котором изменение переменной в некоторой точке времени является линейно коррелированым с предыдущим изменением. Вообще, корреляция уменьшается экспоненциально со временем и исчезает за относительно короткий период. [4]

R / S - анализ стохастических процессов. [5]

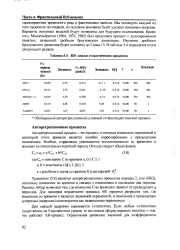
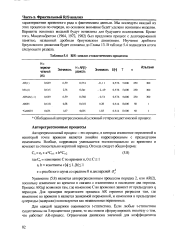
Уравнение (5.8) является авторегрессионным процессом порядка 2, или AR ( 2), поскольку изменение во времени п связано, с изменением в последние два периода. Процесс AR ( q) возможен там, где изменение С во времени п зависит от предыдущих q периодов. Для проверки вероятности процесса AR строится регрессия там, где изменение во времени п является зависимой переменной, и изменения в предыдущие q периоды ( задержки) используются как независимые переменные. [6]

Поскольку ARIMA включает в себя авторегрессионные процессы, модели скользящей средней и интегрирование, то многие динамические процессы можно рассматривать как ARIMA-процессы. В случае 7 ( 1) и 7 ( 2) нужно единожды или дважды рассчитать разности, чтобы получить стационарный ряд. [7]

Считается, что ошибки регрессии представляют собой стационарный авторегрессионный процесс первого порядка. [8]

Для определения параметров о и fi случайного авторегрессионного процесса со скользящим средним ( АРСС) вида ( 24.1 - 4) можно использовать рекуррентный метод наименьших квадратов ( РМНК) ( разд. Поэтому в большинстве случаев предпочтение отдается прямым методам идентификации. [9]

Разработаны модели временных рядов, которые сочетают авторегрессионный процесс с моделью скользящей средней. [10]

В Главе 8 мы видели, что такой авторегрессионный процесс намного менее значим при анализе ежедневных данных. Это дает нам некоторый факт, который соответствует фрактальной гипотезе рынка: информация оказывает различное влияние на различных частотах, и различные инвестиционные горизонты могут иметь различные структуры. В этом, действительно, есть локальная случайность и глобальная структура. На высоких частотах мы можем видеть только чистые стохастические процессы, которые напоминают белый шум. Когда мы делаем шаг назад и смотрим на более низкие частоты, глобальная структура становится очевидной. [11]

Таким образом, h - условная дисперсия - является авторегрессионным процессом квадратов остатков, авторегрессионной условной гетероскедастичостью. [12]

Наиболее важные характеристики гипотезы фрактального рынка имеют дело с убыванием авторегрессионного процесса. [13]

При г Ф 0 регулируемая переменная у ( k) представляет собой авторегрессионный процесс со скользящим средним порядка 2т для РМД1 и порядка т для РМДЗ. [14]

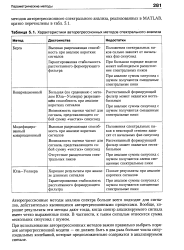Характеристики авторегрессионных методов спектрального анализа. [15]

Страницы: 1 2