Авторегрессионный процесс

Cтраница 2

Авторегрессионные методы анализа спектра больше всего подходят для сигналов, действительно являющихся авторегрессионными процессами. Вообще, хорошие результаты эти методы дают тогда, когда спектр анализируемого сигнала имеет четко выраженные пики. В частности, к таким сигналам относится сумма нескольких синусоид с шумом. [16]

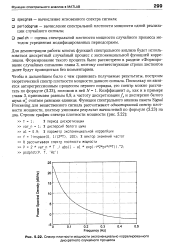Спектр плотности мощности экспоненциально коррелированного дискретного случайного процесса. [17]

Поскольку он является авторегрессионным процессом первого порядка, его спектр можно рассчитать по формуле (5.23), положив в ней N I. Коэффициент alt как и в примере главы 3, принимаем равным 0 9, а частоту дискретизации / д и дисперсию белого шума а2п считаем равными единице. Функции спектрального анализа пакета Signal Processing для вещественного сигнала рассчитывают односторонний спектр плотности мощности, поэтому умножим результат вычислений по формуле (5.23) на два. [18]

R / S-анализ, данные о минимальных колебаниях курса, AR ( 1 S & P. [19]

Во вторых, мы получили важное представление об американской фондовой бирже - представление, которое мы можем применить и к другим рынкам, хотя мы оставляем такой анализ для будущих исследований. Как всегда и предполагалось, при анализе на высокой частоте рынки представляют собой некоторую форму авторегрессионного процесса. Эффект долговременной памяти, видимый на высокой частоте, является настолько маленьким, что он едва виден. [20]

Поскольку проверка справедливости необходимых и достаточных условий - не простая задача, выведен ряд достаточных, легко проверяемых условий однозначности характеризации процесса. Рассмотрены также характеризационные задачи для двух родственных классов систем, а именно систем с шумом типа авторегрессионного процесса и систем, выходной сигнал которых наблюдается в условиях добавления к нему аддитивного шума. Наконец, обсуждаются точность оценки параметров и пределы достижимой точности оценивания при заданном множестве наблюдений. [21]

Совершенно другой подход был предложен Парзеном ( 1969), который не пользовался методом спектральных окон. Одним из главных недостатков этого метода является его частный характер. Несмотря на-то, что рассматривается задача оценивания, отсутствует хорошо определенный критерий. Парзен использует критерий наименьших квадратов, приближает наблюденные данные авторегрессионным процессом и рассматривает спектральную плотность полученного AR-процесса как оценку неизвестной спектральной плотности исходного процесса. Численные результаты, полученные этим методом, оказались достаточно хорошими. [22]

Наиболее полной характеристикой полезного сигнала является е о многомерная плотность распределения, но в некоторых случаях достаточно знать лишь некоторые вероятностные характеристики. Если не ограничиваться классом линейных фильтров, то необходима дополнительная информация. Полезные сигналы х ( t) имеют достаточно полное априорное описание, хотя в измерительной практике встают и задачи определения оценок g [ z ( t) ] - x ( t) при априорной неопределенности. Относительно помех ( f) чаще всего априорные сведения неизвестны, и в данной главе будем пользоваться моделью помех по выражению (6.83) или ее модификациями, а также моделью авторегрессионного процесса. Рассмотрим эту модель подробнее. [23]

Рассмотрим, например, три временных ряда, приводимых в этой книге: среднемесячный расход воды в реке из гл. Все эти ряды обладают систематическими периодическими колебаниями и не имеют характера процессов роста. Тем не менее соответствующие им модели имеют совершенно разную структуру. Последовательность ежемесячных наблюдений речного потока моделируется авторегрессионной моделью первого или второго порядка для у с добавлением синусоидальных членов. Удовлетворительной моделью численности популяции рысей является авторегрессионная модель для переменной log у с добавлением синусоидальных членов. Наконец, последовательность чисел солнечных пятен хорошо описывается авторегрессионным процессом высокого порядка с авторегрессионными членами типа y ( t - [ Т - 11), где Т - период доминирующего колебания, а [ Т - 1 ] - ближайшее целое к Т-1 число. Необходимости в добавлении синусоидальных членов не возникает. [24]

Страницы: 1 2