Псевдочастота

Cтраница 1

Псевдочастота Я в этой области практически совпадает с частотой со входного сигнала. [1]

О псевдочастота v принимает большие значения. Это значит, что при использовании логарифмических характеристик практически невозможно исследовать их поведение в области малых частот со. [2]

Матрично-структурная схема. [3]

В области псевдочастоты запасы по фазе и амплитуде становятся надежными характеристиками качества дискретной системы. [4]

Задаваясь различными значениями псевдочастоты о ( от 0 до оо), получим годограф W ( jv), изображенный на рис. 6.10, а. Как видно из рисунка, годограф полуохватывает точку ( - 1; / 0) в отрицательном направлении V2 раза, что указывает на неустойчивость импульсной системы автоматического регулирования в замкнутом состоянии. [5]

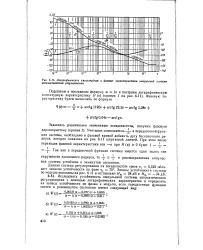Логарифмические амплитудные и фазовые характеристики импульсной системы автоматического регулирования. [6]

Задаваясь различными значениями псевдочастоты, получим фазовую характеристику ( кривая 2), Учитывая сомножитель -: - в передаточной функции системы, необходимо в фазовой кривой добавить дугу бесконечного радиуса, которая показана на рис. 6.11 штриховой линией. [7]

Структурная схема одного контура управления. [8]

Использование - преобразования и псевдочастоты А позволяет привести передаточную функцию к виду, удобному для применения метода логарифмических частотных характеристик. [9]

Будем определять ю пр1 как значение псевдочастоты со, при которой ( 3 - 50) обращается в точное равенство. [10]

При первом способе по оси абсцисс откладывается псевдочастота v, причем деления на оси наносятся в логарифмическом масштабе. [11]

Можно, впрочем, определив несколько иным способом понятие условной псевдочастоты, так усовершенствовать машину условной вероятности, что в ней сразу будут определяться условные псевдочастоты свойств без предварительного вычисления и запоминания их безусловных частот или псевдочастот. [12]

Рассмотрим способ такого построения ЛАЧХ импульсной системы в указанном диапазоне псевдочастот. Наиболее часто имеет место случай, когда ЛАЧХ, соответствующая WBT ( P), является асимптотой с наклоном - 20 дБ / дек, дополненной отрезками асимптот с сопрягающими частотами, большими предельной частоты. [13]

Для ДАС с более сложными непрерывными частями частотные характеристики при использовании псевдочастоты строятся с меньшими вычислительными трудностями. [14]

Более удобно для получения частотных характеристик и, в частности, логарифмических характеристик использовать псевдочастоту. [15]

Страницы: 1 2 3