Путь - интегрирование
Cтраница 4
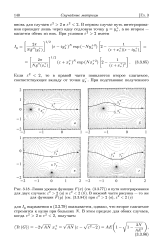 |
Линии уровня функции F ( x ( и пути интегрирования. [46] |
В первом случае путь интегрирования проходит лишь через одну седловую точку у у, а во втором - касается обеих из них. [47]
При решении выбрать путь интегрирования, соединяющий точки М и N, М и Р так, чтобы он не пронизывал контур с током. [48]
Во многих случаях путь интегрирования приходится выбирать в комплексной плоскости. [49]
При решении выбрать путь интегрирования, соединяющий точки т и п, т и р так, чтобы он не пронизывал контур с током. [50]
В таком интеграле путь интегрирования в плоскости комплексной переменной г проходит под точкой z i6 -, при б - 0 это эквивалентно интегрированию вдоль вещественной оси с обходом полюса z 0 по бесконечно малой полуокружности снизу. [51]
Положим, что путь интегрирования совпадает с осью оу. [52]
Пусть С - путь интегрирования, М0 - его начальная, М - конечная точка; М, М - точки на этом пути. [53]
Разумеется, форма пути интегрирования от точки А до точки М здесь безразлична, так как под знаком интеграла находится полный дифференциал. [54]
Страницы: 1 2 3 4