Непрерывный путь

Cтраница 2

Профиль как зажимающих поверхностей, так и прокладок должен быть таков, чтобы с обеих сторон прокладки находился по крайней мере один непрерывный путь деформации, проникающей глубже, чем дефекты поверхности прокладки. [16]

Так как V связно и локально евклидово, то любые две точки р0 и pl этого многообразия всегда можно соединить при помощи непрерывного пути. Согласно лемме Бореля-Лебега, его можно покрыть конечным числом областей А. Отсюда вытекает, что для каждой пары областей Д0 и AJ из Д существует конечная цепочка ( последовательность) областей Д, начинающаяся с Д0, кончающаяся в Д [ и такая, что две последовательные области этой цепочки всегда имеют общие внутренние точки. [17]

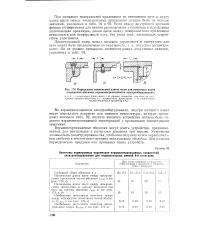Определение наименьшей длины щели для некоторых видов сопряжений оболочек взрывонепроницаемого электрооборудования. [18]

Если между внутренней кромкой фланца и отверстиями для винтов располагается утопленная в тело фланца уплотняющая прокладка, длина щели между поверхностями прилегания исчисляется как непрерывный путь, без учета мест, занимаемых устройством уплотнения. [19]

В первом случае, когда твердое хрупкие зерна карбида изолированы ( см. фиг. В последнем случае карбидные пластины образуют почти непрерывный путь, по которому может происходить разрушение металла ( см. фиг. Такое упрощенное сравнение может служить основой для анализа различий в свойствах. Сплав, в микроструктуре которого имеются сфероидизированные частицы второй фазы, характеризуется более высокой вязкостью, потому что траектория разрушения должна проходить как через хрупкие частицы карбидов, так и через вязкий, способный деформироваться феррит. Такая сталь также более пластична, потому что имеется большая возможность для пластической деформации и поглощения энергии деформации вдоль траектории возможного разрушения. В противоположность этому сталь с пластинчатой структурой прочнее и тверже, чем со сфероидизированной, потому что в этом случае мягкая ферритная матрица в большей степени армирована частицами твердой карбидной фазы. [20]

Возьмем теперь произвольную точку А поверхности &, проведем в этой точке нормаль к поверхности и выберем на этой нормали какое-нибудь определенное из двух возможных направлений. Будем перемещать точку А по поверхности S, следуя по любому непрерывному пути, и при этом в каждой точке, через которую мы проходим, приписывать нормали к поверхности то из двух возможных направлений, с которым мы по непрерывности приходим в нее, следуя по нашему пути. Допустим, что, пройдя таким образом некоторый путь, мы возвращаемся в точку А. [21]

Соответствующее уравнение в гидродинамике называется Уравнением Непрерывности. Оно не может просто исчезнуть в одном месте и появиться в другом, а должно пройти по некоторому непрерывному пути, так что, если провести замкнутую поверхность, включающую одно местоположение и исключающую другое, материальное вещество, переходя из этого одного положения в другое, должно пройти через эту замкнутую поверхность. [22]

Пусть асимптотическое решение z za ( t) ( lirn za ( t) ZQ) невозмущенной системы продолжается однозначно и аналитически вдоль замкнутого непрерывного пути 7: [0,1] - С. [23]

Еще, раз следует подчеркнуть, что каждый пример выпуклого множества - ото и пример линейно связного множества. Невыпук-лым линейно связню множеством является, например, любая сфера в 1РЧК при чх д, Другой очевидный ( но, как ни странно, более общий) пример: траектория непрерывного пути. Запас примеров линейно связных МНОЖ ГЧРВ можно существенно увеличить с помощью следующего утверждения. [24]

Для установления связности достаточно рассмотреть две точки на М2, являющиеся концами одного и того же нормального отрезка, и предъявить на М2 путь, соединяющий эти две точки. Тогда, дополнив этот репер третьим вектором, ортогональным к ЕР2, и рассмотрев след этого вектора, высекаемый им при непрерывном передвижении репера по замкнутому пути, мы и получаем на М2 непрерывный путь, соединяющий две выбранные нами точки. [25]

Так, для пены, содержащей менее 1 % ( об.) воды ( остальное - воздух), дисперсионной средой является вода, поскольку по водным пленкам можно пройти из любой точки в любую другую, тогда как по воздушной дисперсной фазе непрерывного пути нет. Однако в капиллярно-пористых телах часто обе фазы-и твердый каркас, и совокупность пор - являются непрерывными и одновременно удовлетворяют условию дисперсионной среды. [26]

Так, для пены, содержащей менее 1 % ( об.) воды ( остальное - воздух), дисперсионной средой является вода, поскольку по водным пленкам можно пройти из любой точки в любую другую, тогда как по воздушной дисперсной фазе непрерывного пути нет. Однако в капиллярно-пористых телах часто обе фазы - и твердый каркас, и совокупность пор - являются непрерывными и одновременно удовлетворяют условию дисперсионной среды. [27]

То же самое можно выразить иначе: всякое такое множество имеет хотя бы одну граничную точку. Траектория непрерывного пути может оказаться вовсе не тем, что хотелось бы считать кривой линией. Покажите, jo ни одно из таких отображений не мож т быть взаимна однозначным. Докажите, что если удалить из пространства ( размерности А) какой угодно счетный набор точек останется линейно связно множество. [28]

Следовательно, по теории Бошковича, атом имеет непрерывное существование во времени и в пространстве. В каждое мгновение он находится в некоторой точке пространства, и не более как в одном месте в одно и то же время. Он переходит из одного места в другое по непрерывному пути. Он имеет определенную массу, которая неспособна ни к увеличению, ни к уменьшению. Атомы одарены способностью действовать друг на друга притягательно либо отталкивательно, причем величина силы зависит от расстояния между ними. С другой стороны, сам атом не имеет частей или размеров. [29]

Из различных форм атомистической теории теория Бош-ковича может быть приведена как пример чистейшей монадологии. Согласно Бошковичу, материя составлена из атомов. Каждый атом есть неделимая точка, имеющая положение в пространстве, способная к движению по непрерывному пути и обладающая известной массой, вследствие чего потребно известное количество силы, чтобы произвести данное изменение движения. [30]

Страницы: 1 2 3