Геодезический путь
Cтраница 1
Геодезический путь - это путь, являющийся локально оптимальным и, следовательно, не поддающийся укорачиванию посредством небольших вариаций. Заметим, что такой путь не может проходить через концы какого-либо из ребер ei, поскольку в противном случае два разных последовательных ребра из & должны были бы быть коллинеарны. [1]
Геодезический путь не может быть определен только лишь заданием положения и направления одного его элемента, ибо из данного положения в данном направлении возможно провести бесконечное число геодезических путей. [2]
Лемма 3.1. Всегда существует геодезический путь из точки s до любой другой точки х е У. [3]
Из определений нельзя заключить, что каждый геодезический путь является также кратчайшим путем, и простые примеры показывают, что существуют геодезические пути, которые не являются одновременно кратчайшими путями между данными концевыми положениями. [4]
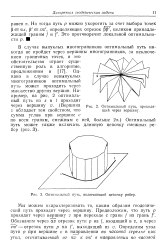 |
Оптимальный путь, включающий цепочку ребер. [5] |
Мы можем охарактеризовать то, каким образом геодезический путь проходит через вершину. [6]
Обратите внимание на то, что пересечение геодезического пути с гранью может быть объединением нескольких отдельных прямолинейных отрезков. Например, если несколько раз обмотать туго натянутую струну вокруг длинного узкого прямоугольного параллелепипеда, то путь, по которому она пройдет, локально будет оптимален, хотя глобально, конечно, нет. [7]
Кратчайший путь между двумя положениями есть геодезический, но геодезический путь не есть обязательно кратчайший, хотя он всегда есть кратчайший между любыми двумя достаточно близкими соседними его положениями, находящимися на конечном удалении друг от друга. [8]
Для каждого интеграла дифференциальных уравнений материальной системы число постоянных, которые определяют геодезический путь, уменьшается на два. [9]
Между двумя любыми возможными положениями всегда возможен, по крайней мере, один геодезический путь ( пп. [10]
Эти уравнения, являющиеся необходимыми условиями для исчезания вариаций, выполняются, следовательно, для всех положений геодезического пути; таким образом, они содержат решение поставленной задачи. [11]
Сейчас мы сформулируем одно простое свойство геодезических ( оно упоминается в работах [7] и [17]), заключающееся в том, что при развертке геодезического пути вдоль реберной последовательности он переходит в отрезок прямой. [12]
Геодезический путь не может быть определен только лишь заданием положения и направления одного его элемента, ибо из данного положения в данном направлении возможно провести бесконечное число геодезических путей. [13]
Впрочем, эти 2г - 21 произвольных постоянных все же достаточны, как это и должно быть, для того чтобы каждое возможное положение связать с каждым другим возможным положением посредством геодезического пути, ибо если между ре существует Z конечных уравнений, то достаточно провести путь так, чтобы два его положения имели г - / общих координат с каждым данным положением. [14]
Если теперь мы будем сближать оба положения вдоль рассматриваемого геодезического пути, то длина этого пути и одновременно длина абсолютного кратчайшего пути будут стремиться к нулю, в то время как остальные геодезические пути остаются конечными. По крайней мере, начиная от некоторого конечного расстояния между положениями, геодезический путь, вдоль которого оба положения сближаются, должен совпасть с абсолютно кратчайшим из них. [15]
Страницы: 1 2