Пучок - параллельная прямая
Cтраница 1
Пучок параллельных прямых определяет два направления. [1]
Рассмотрим пучок параллельных прямых y kx b, где k i / m, каждая из которых пересекает С0 и С не более чем в одной точке. [2]
При проведении перспективы пучка параллельных прямых, имеющих общую точку схода, рекомендуется пользоваться установленной в этой точке тонкой швейной иглой № 0 или № 1, к которой и прикладывается линейка для проведения линий в эту точку схода. Прежде чем выполнять упражнения, необходимо изучить данный материал по учебнику. [3]
Сколько различных направлений определяет пучок параллельных прямых. [4]
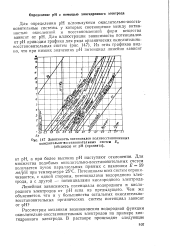 |
Зависимость потенциалов полувосстановленных окислительно-восстановительных систем Е ( абсцисса от рН ( ордината. [5] |
Для множества подобных окислительно-восстановительных систем получается пучок параллельных прямых с наклоном Е 59 жв / рН при температуре 25 С. [6]
Если прямая перпендикулярна одной из прямых пучка параллельных прямых, то она перпендикулярна любой другой прямой этсго пучка. [7]
Если прямая перпендикулярна одной из прямых пучка параллельных прямых, то она перпендикулярна любой другой прямой этого пучка. [8]
Множество прямых аффинной плоскости разбивается на п-т пучок параллельных прямых по п прямых в каждом. Сопоставим ему граф Г; на множестве вершин 5s, в котором пара точек соединена ребром тогда и только тогда, когда проходящая через них прямая принадлежит Si. Клин показали, что аффинное клеточное кольцо обладает замечательным свойством: любое разбиение множества его антирефлексивных образующих порождает клеточное кольцо. [9]
С в оо, то эти окружности преобразуются в пучок параллельных прямых. [10]
Поскольку любое аффинное преобразование переводит любое направление на плоскости ( пучок параллельных прямых) снова в некоторое направление, имеет смысл говорить об аффинных преобразованиях, оставляющих на месте данное направление со. [11]
Замечая, что линии контура плана могут быть разделены на два пучка параллельных прямых, определяем перспективы несобственных точек ( F1 и F2) каждого из пучков, причем точка F1 является перспективой несобственной точки пучка параллельных прямых направления I, а точка F2 - направления II. Обе точки найдены при помощи лучей SF1 и SF2, соответственно параллельных прямым направлений I и II. [12]
Кривая в плоскости Лобачевского называется орициклом, если она пересекает под прямым углом пучок параллельных прямых. [13]
Будучи общей горизонталью вспомогательных плоскостей, прямая S S2 определяет направление их горизонтальных следов, которые в данном случае образуют пучок параллельных прямых. Определим точки пересечения ребер первой пирамиды S ABC с гранями второй StDEF. Проводя вспомогательные плоскости через ребра 5S и S C, замечаем, что следы плоскостей РгН и Pifl не пересекают основания второй пирамиды. [14]
Геометрическая идея доказательства состоит в том, что фиксируется узел / (, а меняется проекция. Каждый пучок параллельных прямых в 3 определяет проекцию пространства Я3 на плоскость, проходящую через начало координат перпендикулярно рассматриваемому пучку. [15]
Страницы: 1 2