Работа - поверхностная сила
Cтраница 1
Работа поверхностных сил расходуется на трение вихря о стенки капилляра и внутреннее трение в объеме электролита ЭЯ из-за его вязкости. [1]
Вычислим работу поверхностных сил. [2]
Это значит, что работа поверхностных сил равна сумме элементарной работы перемещений избытка напряжений поверхностных сил и работы деформаций. [3]
Чистый приток энергии, обусловленный работой поверхностных сил. [4]
Внешнее воздействие на выделенную ячейку определяется работой поверхностных сил - nr pbwb, потоком тепла 4лг % дь и диффузией компонент 4яг ( рум. [5]
Для простоты дальнейших рассуждений считаем, что работа поверхностных сил иа гранях C0j и со2 равна нулю. Это возможно, если на ш, и ш2 отсутствует поверхностная нагрузка, либо если эти грани закреплены. [6]
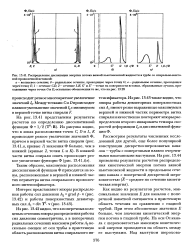 |
Распределение диссипации энергии потока вязкой ньютоновской жидкости в трубе со спирально-винтовой проволочной вставкой. [7] |
Из рис. 13.43 также видно, что эпюры работы девиаторных поверхностных сил А. [8]
Энергия объема V изменяется не только за счет работы объемных и поверхностных сил, приложенных к объему, но и за счет отдачи тепла в окружающую среду и на фазовые превращения. [9]
 |
Течение в трубке тока. [10] |
В уравнении ( 20) опущено слагаемое, описывающее работу поверхностных сил. В большинстве практических случаев при соответствующем выборе контрольного объема эта работа оказывается пренебрежимо малой. [11]
Не приводя этих рассуждений, по аналогии напишем, что работа касательных поверхностных сил равна - gkMdh, где dh - потери энергии на трение, приходящиеся на единицу веса жидкости или газа. [12]
Члены в правой части уравнения (5.5) физически представляют собой соответственно работу поверхностных сил, работу объемных сил, кинетическую энергию и работу внутренних сил. При выводе (5.5) предполагалось, что область D не зависит от времени. [13]
Здесь двойной интеграл, распространенный по поверхности тела, представляет работу поверхностных сил, тройной интеграл - работу объемных сил. [14]
Первый интеграл левой части, как уже было сказано, выражает удвоенную работу поверхностных сил, совершенную в процессе деформации; второй интеграл выражает удвоенную работу объемных сил; в правой части стоит удвоенная потенциальная упругая энергия. Очевидно, что соотношение (5.62) формулирует предположение, сделанное в начале § 20 гл. III о существовании потенциала упругих сил; согласно этой гипотезе, работа поверхностных и объемных сил должна быть полностью накоплена в форме упругой потенциальной энергии. [15]
Страницы: 1 2 3