Виртуальная работа

Cтраница 1

Виртуальная работа дА сторонних и диссипативных сил также выражается в переменных кг. [1]

Виртуальная работа разрушения 6Л / равна сумме работы, затрачиваемой на разрушение матричной прослойки, и работы, идущей на продвижение трещины в отслоении. [2]

Виртуальная работа At упругих сил на возможном перемещении 6г / равна приращению энергии деформации с обратным знаком. [3]

Виртуальная работа сил реакции связи будет равна нулю, так как точка приложения силы реакции неподвижна. [4]

Сумма виртуальных работ всех сил в системе должна равняться нулю. [5]

Принцип виртуальной работы записывается следующим образом ( ср. [6]

Принцип виртуальных работ ( 1) справедлив для произвольных определяющих соотношений. [7]

Принцип виртуальных работ может служить для вывода общей энергетической теоремы. [8]

Принцип виртуальных работ, в своей наиболее общей форме, приложим как к статическим, так и к динамическим задачам. [9]

Вычислим возможную и виртуальную работу. [10]

Так как виртуальная работа произвольной системы сил, действующих на данное твердое тело, зависит лишь от двух величин: равнодействующей силы F и результирующего момента М, то мы сразу получаем важную теорему: две системы сил с равной равнодействующей и равным результирующим моментом механически эквивалентны. [11]

При определении виртуальной работы этот внутренний момент также формально относят к числу внешних воздействий. [12]

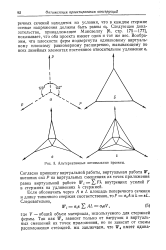Альтернативные оптимальные проекты. [13]

Согласно принципу виртуальной работы, виртуальная работа Wе внешних сил Р на виртуальных смещениях их точек приложения равна виртуальной работе Wt FK внутренних усилий F в стержнях на удлинениях Я стержней. [14]

Это принцип виртуальной работы, выраженный в общих криволинейных координатах. [15]

Страницы: 1 2 3 4