Характеристический вектор
Cтраница 1
Характеристические векторы полезны в том случае, когда формирование нужной подпоследовательности выполняется путем последовательного удаления из основной последовательности элементов, которые не входят в подпоследовательность. Главное неудобство характеристических векторов состоит в том, что они не экономичны. [1]
Характеристические векторы полезны в ряде случаев метода решета, которые обсуждаются в разд. Вообще их полезность вытекает из их компактности, существования простого фиксированного соотношения между i и адресом t - го разряда и возможности при таком представлении очень легко исключать элементы. Действительно, все примеры из разд. [2]
 |
Прямолинейные пути реакции в роли осей координат для характеристических веществ В ] в симплексе реакции. [3] |
Характеристические векторы состава полностью описаны в пространстве составов. [4]
Характеристические векторы X; и z называются соответственно правым и левым характеристическими векторами матрицы К. Векторы z, и х, соответствующие одному и тому же характеристическому корню - К, будут равны только. К симметрична; этот случай является редким. Поэтому для каждого правого характеристического вектора х, с Х 0 имеется левый характеристический вектор z; с A. Все векторы с Я 0, конечно, инвариантны по времени; те из них, которые соответствуют правым характеристическим векторам х -, приводят к инвариантности равновесного состава по времени, а соответствующие левым характеристическим векторам z; накладывают ограничения на систему. [5]
Вычислим характеристический вектор множества A U В. [6]
Годограф характеристического вектора в плоскости комплексного переменного при изменении частоты со от - оо до х называется амплитудно-фазовой характеристикой системы или ее элемента. [7]
Вращение характеристического вектора М ( / со) вызывает чередование точек пересечения годографа с вещественной и мнимой осями. [8]
Множество характеристических векторов функции ф называется характеристическим множеством этой функции. [9]
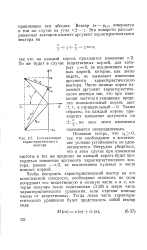 |
Составляющие так что необходимое и достаточное условие устойчивости не удовлетворяется. Нетрудно убедиться, что в этом случае при изменении. [10] |
Чтобы построить характеристический вектор на его комплексной плоскости, необходимо отложить по осям координат его вещественную и мнимую части и и о, которые получим после подстановки (3.28) в левую часть характеристического уравнения, если отделим мнимые члены от вещественных. [11]
Если годограф характеристического вектора удовлетворяет требованиям критерия Михайлова, то такой годограф и его протекание называются правильными, в противном случае - неправильными. [12]
Если годограф характеристического вектора удовлетворяет требованиям критерия Михайлова, то такой годограф и его протекание называются правильными, в противном случае - неправильными. [13]
Эта независимость характеристического вектора ш от выбора полюса может быть установлена и непосредственно. С этой целью покажем прежде всего, что угловая скорость о не изменяется, когда мы изменяем направление подвижных осей при том же полюсе О. [14]
Главное неудобство характеристических векторов состоит в том, что они не экономичны. [15]
Страницы: 1 2 3 4