Радиус - сольватированный ион
Cтраница 1
Радиус сольватированного иона, вычисленный по уравнению Стокса, оказался равным 5 - 10 - 8 см, что хорошо согласуется с литературными данными. [1]
Действительно, произведение радиуса сольватированного иона ( см. параграф 1.4.1) на макровязкость растворителя и подвижность иона гораздо лучше сохраняет постоянство, чем вальденовское произведение. [3]
Было также предложено [103] радиус сольватированного иона рассчитывать, используя полуэмпирическое соотношение, основанное на законе Стокса. [4]
Аво-гадро, г - - радиус сольватированного иона, DHZO и DM - диэлектрические проницаемости в водном и неводном растворах, Дм; - разница в энергиях ион-ипольного взаимодействия в водном и смешанном растворах) можно прийти к выводу, что первое слагаемое в левой части (V.90) должно уменьшаться при повышении температуры. Второе слагаемое должно, согласно теории Дебая - Хюккеля, с ростом температуры незначительно увеличиваться. [5]
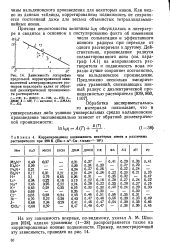
Общая толщина двойного слоя ц слагается из толщины 60, отвечающей приблизительно радиусу сольватированного иона ( плотная часть двойного слоя), и толщины К размытой части: ( д, б Я. Величина К зависит от природы и особенно от концентрации раствора. [6]
 |
Изменение эквивалентной концентрации катионов Ск и анионов Са в двойном слое при размытом строении его. [7] |
Общая толщина двойного слоя ц слагается из толщины бо, отвечающей приблизительно радиусу сольватированного иона ( плотная часть двойного слоя), и толщины Я, размытой части: jj, бо - - К. Величина Я, зависит от природы и особенно от концентрации раствора. [8]
Емкость диффузного строения двойного электрического слоя ( для разбавленных растворов) определяется не величиной радиуса сольватированных ионов, равной толщине плотной части двойного слоя, а эффективной толщиной двойного слоя d, возрастающей с увеличением его диффузной части и приводящей к уменьшению емкости. Размыв двойного слоя наиболее заметно выражен, когда состояние электрода близко к точке нулевого заряда. Рассчитанные значения емкости существенно превышают величины емкостей обычных конденсаторов, что объясняется, по-видимому, весьма малой толщиной ( б или d) двойного слоя. [9]
Наименьшее расстояние а, на которое могут сблизиться ионы, невозможно установить независимым путем, поскольку неизвестны радиусы сольватированных ионов, оболочки которых могут перекрываться, а также и потому, что эта величина - результат сложного усреднения для различных контактирующих ионов С - А -, С - С и 4 - А -, Ее рассматривают как параметр, подлежащий уточнению, Наилучшее согласие теории с экспериментом достигается при а, несколько превышающих сумму кристаллографических ионных радиусов, например для NaC а - 4 5 А, тогда как сумма кристаллографических радиусов для этой соли составляет rNa rcl - 2 76 Х - При очень низкой ионной силе / ( т.е. при а В. [10]
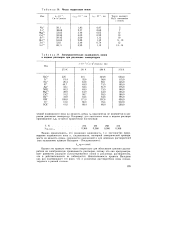 |
Числа гидратации ионов.| Электролитическая подвижность ионов в водных растворах при различных температурах. [11] |
Однако это правило очень часто непригодно для объяснения влияния растворителя на электрическую проводимость растворов, потому что оно предусматривает равенство радиусов сольватированных ионов в различных растворителях, что в действительности не соблюдается. Невыполнимость правила Вальдена как раз подтверждает тот факт, что в различных растворителях ионы сольва-тируются в разной степени. [12]
В результате существенного расширения представлений о природе и характере зависимости диэлектрической проницаемости среды вблизи иона от напряженности поля и о размерах радиусов сольватированных ионов появилась возможность максимально строгой проверки чисто электростатической теории сольватации. Оказалось, что даже простая борновская модель сольватации, усовершенствованная в свете новейших достижений теории и эксперимента, может вполне удовлетворительно описать наблюдаемые закономерности. Не вдаваясь в детали выводов и расчетов, рассмотрим кратко результаты некоторых работ, в которых учтены эффекты диэлектрического насыщения при расчетах энергетики сольватации ионов. [13]
Рассматривая связь гидрахных чисел с размерами ионов, автор работы [5] нашел, что гидратные числа приблизительно пропорциональны плотности электростатической энергии на поверхности иона. Там же [5] получено соотношение между h и радиусом сольватированного иона и впервые термодинамически обоснована зависимость ближней гидратации иона от его заряда и радиуса. Вместе с тем отмечается [66, 68], что уравнение (4.2) нельзя рассматривать как вполне удовлетворительное, так как концепция гидратных чисел является слишком большим упрощением. [14]
 |
Молярные электропроводности ионов в бесконечно разбавленных водных растворах при 25 С. [15] |
Страницы: 1 2