Радиус - кривизна - волновой фронт
Cтраница 1
Радиус кривизны волнового фронта считаем положительным ( R 0) для расходящейся волны, отрицательным ( R С 0) для сходящейся. [1]
Изменяются только ширины пучков и радиусы кривизны волновых фронтов. [2]
Таким образом, в реальных ситуациях радиусы кривизны волновых фронтов в точке ZQ для всех эрмит-гауссовых пучков вида (1.91) одинаковы. Это очень существенное обстоятельство, поскольку выше было сформулировано простое правило ( правило ABCD, § 1.5) для определения радиуса кривизны волнового фронта простого гауссова пучка ( основной моды); у высших поперечных мод радиусы кривизны такие же, как у основной моды. [3]
R, следовательно, играет роль радиуса кривизны сферического волнового фронта. Если z J kw, то R г, что соответствует дифракции Фраунгофера. Если z kwl ( дифракция Френеля), то R ( kwlYfz и при г - 0 волновой фронт переходит в плоский. [4]
Каждое поперечное сечение z такого резонаторного пучка характеризуется радиусом кривизны сферического волнового фронта Rz и расстоянием wz от оси, на котором амплитуда основной моды уменьшается в е раз. [5]
Очевидно, что Bl / R, где R - радиус кривизны волнового фронта, a Df - характерная ширина пучка. [6]
 |
Вид сбоку на гауссов пучок. Показаны волновые фронты, перетяжка, рэлеев. [7] |
Из выражения ( 7.7.2 а) непосредственно следует, что радиус кривизны волнового фронта R ( z) z Ъ 2 / z в перетяжке становится очень большим. [8]
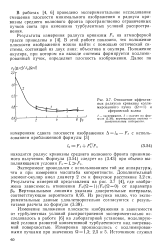 |
Отношение эффективных радиусов кривизны колли-мированного пучка ( Q l и сферической волны. [9] |
В работах [4, 6] проведено экспериментальное исследование смещения плоскости минимального изображения и радиуса кривизны среднего волнового фронта пространственно ограниченных пучков света при изменении турбулентных условий распространения. [10]
Нетрудно убедиться, что для этого пучка имеют место те же самые выражения (1.52) и (1.53) для радиуса кривизны волнового фронта и поперечного радиуса. [11]
Однако приведенное выше физическое обоснование указанных методов, апеллирующее к сходству изменений комплексного параметра гауссова пучка q и радиуса кривизны волнового фронта R, нельзя считать достаточно строгим. [12]
Для безаберрационного восстановления исходного волнового фронта необходимо, чтобы восстанавливающий пучок имел то же направление распространения и тот же радиус кривизны волнового фронта, что и опорный пучок, использовавшийся при получении голограммы. Разрешение изображения, образованного восстановленной волной, ограничивается протяженностью голограммы и когерентными свойствами восстанавливающего пучка. [13]
Как эрмито-гауссовые, так и лагерро-гауссовые моды, реализуемые на практике, характеризуются, как правило, большим значением радиуса кривизны волнового фронта. [14]
Характеристики квазиоптического пучка могут быть изменены с помощью фазового корректора с геометрическим фокусным расстоянием F ( рис. 3.16); радиус кривизны преобразуется по закону F - - l j - Г где Ri я Rz - радиусы кривизны волнового фронта слева и оправа от фазового корректора. [15]
Страницы: 1 2