Радиус - покрытие
Cтраница 1
Радиус покрытия R определяется равенством ( 3) гл. В процессе доказательства теоремы 1 мы расклассифицируем все глубокие дыры ( их определение см. в разд. Имеется замечательная связь между этими дырами и решетками Нимейера. Решетка Лича представляет собой единственную 24-мерную четную унимодулярную решетку с минимальной нормой 4 ( гл. [1]
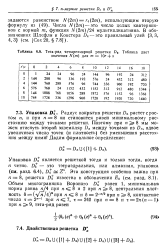 |
Тэта-ряд четырехмерной решетки D. [ TABLE ] дает значения N ( т для от 10r s. [2] |
Радиус покрытия решетки Dn растет с ростом п, и при п 8 ои становится равен минимальному расстоянию между точками решетки. [3]
Ее радиус покрытия будет определен в следующем параграфе. [4]
Проблема определения радиуса покрытия решетки Лича решается в следующей главе, написанной Конвеем, Паркером и Слоэном. До того как был открыт подход, используемый ими, было получено описанное в этой главе хорошее приближение к истинному значению. Оно заслуживает описания не только по историческим причинам и потому, что доказательство является очень коротким; важно, что используемый метод не зависит от свойств решетки Лича и, следовательно, может быть применен к другим решеткам. [5]
Для t 3 о радиусе покрытия ранее было известно очень немного. [6]
Показано, что проблема нахождения радиуса покрытия и минимального расстояния алгебраических и арифметических кодов связана с проблемой Ва-ринга и теорией циклотомических чисел. Предложенные методы приводят к новым результатам для радиуса покрытия некоторых кодов БЧХ, исправляющих t ошибок. Кроме того, получены новые результаты для радиуса покрытия и минимального расстояния некоторых классов арифметических кодов, порожденных простыми числами. [7]
Совершенный код определяется условием равенства радиуса покрытия и радиуса упаковки. [8]
Теорема Дельсарта [7] утверждает, что радиус покрытия кода не превосходит числа ненулевых весов в двойственном к нему коде. [9]
В этой главе описывается метод оценки радиуса покрытия решетки. При его применении к решетке Лича получается весьма близкое к истинному значение. [10]
Другой путь, приводящий к хорошим верхним границам радиуса покрытия, основан на теории циклотомических чисел. [11]
Вскоре после открытия своей решетки Джон Лич высказал предположение, что ее радиус покрытия в - у / 2 раз больше, чем ее радиус упаковки, но не сумел это доказать. [12]
Пусть р ( К А) и У ( Кв) обозначают радиус покрытия кода КА и число ненулевых весов, встретившихся в двойственном коде KB соответственно. [13]
Мы ссылались выше на относящийся к алгебраическим кодам результат Дельсарта [7], утверждающий, что радиус покрытия кода не превосходит числа ненулевых весов в двойственном коде. В связи с этим возникает естественный вопрос, справедливо ли аналогичное утверждение для арифметических кодов. Мы приведем контрпример, показывающий, что в этом случае ответ отрицательный. [14]
Тогда Лп - ь которое мы будем называть радиусом подпокрытия, является нижней границей для радиуса покрытия / v - i решетки Лл-1. Несложно гадеть, что hn - и rn-i равны, если любое из этих чисел д / 3 - ( Представляется правдоподобным, что hn - всегда равно rn-i, хотя мы и не можем этого доказать. [15]
Страницы: 1 2 3