Радиус - стержень
Cтраница 3
Распределение энергии по поперечному сечению волновода, содержащего ферритовый стержень на фиксированной частоте, зависит [85, 231] от магнитной проницаемости и диэлектрической постоянной материала, а также от отношения радиусов стержня и волновода. В случае нулевой намагниченности распределение одинаково для обоих направлений вращения круговой поляризации. [31]
Результаты приведены в безразмерной форме: отношение с / сй дано для различных значений отношения а / Л ( здесь с - фазовая скорость волн с длиной A, CQ - скорость продольных волн с бесконечной длиной волны и а - радиус стержня; сравнить с фиг. Можно видеть, что согласие очень хорошее за исключением нескольких отдельных точек, которые, невидимому, соответствуют другим формам колебаний. Одна из основных трудностей экспериментального исследования состоит в том, что возбуждаемые в цилиндрах изгибные, крутильные и продольные волны возникают, вообще говоря, одновременно и наблюдаемая волновая картина становится очень сложной. [32]
О направлении касательных напряжений мы можем судить, исходя из следующих соображений: так как на боковой поверхности стержня нет касательной нагрузки, то там не может быть и касательных напряжений, - следовательно, в точках у контура сечения по закону парности не может быть касательных напряжений, направленных параллельно радиусу стержня. У контура сечения направление касательных напряжений может быть только перпендикулярно к радиусу круга. Естественно предположить, что и во всех остальных точках сечения напряжения сохраняют направление, перпендикулярное к соответствующему радиусу. [33]
Если согнуть прямолинейный стержень в круговое кольцо и привести это кольцо во вращение относительно перпендикулярной к его средней плоскости оси симметрии то каждый малый отрезок этого кольца приближенно находится в тех же условиях, что и рассмотренный отрезок прямого стержня, если предположить, что радиус кривизны кольца велик по сравнению с радиусом стержня. То же будет справедливым и для дискообразного кругового кольца, если только радиус ограничивающего его изнутри цилиндра не слишком мал. [34]
Как и в случае стержня Гопкинсона, аппаратура Девиса дает правильную запись давления, приложенного к нему, лишь тогда, когда а) напряжение нигде не превышает предела упругости стали и б) давление не изменяется настолько быстро, что длины волн, связанных с импульсом давления, становятся сравнимыми с радиусом стержня. [35]
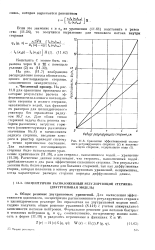 |
Сравнение зффективностей сплошного регулирующего стержня ( 1 и поглощающего стержня, содержащего воду ( 2. [36] |
На рис. 11.8 для сравнения приведены некоторые результаты расчета эффективности сплошного поглощающего стержня и полого стержня, заполненного водой, как функций irx размеров для цилиндрического реактора без отражателя радиусом 36 7 см. Для обоих типов стержней задача была решена выбором различных загрузок горючего ( соответствующих различным значениям fk / k) и вычислением радиуса стержня, введение которого в реактор приводит систему в точно критическое состояние. [37]
Для отрицательной волны передаваемая энергия концентрируется в ферри-товом стержне; поэтому, хотя в данном случае потери не слишком велики, они все же растут при наличии диэлектрических колебаний, тогда как для положительной волны имеет место обратное явление. При увеличении же радиуса стержня может оказаться, что он превзойдет глубину поверхностного эффекта, и тогда поле положительной волны будет не полностью пронизывать феррит. Оба эффекта уменьшают величину R по сравнению с теоретической. [38]
Поскольку, однако, величина Ъ часто бывает того же порядка, что и величина транспортной длины, свободного пробега в активной зоне А, или намного меньше ее, обычное соотношение (5.71), вообще говоря, неприменимо. Для промежуточных значений радиуса стержня величину е можно определить по кривой рис. 11.3. Поток нейтронов вблизи стержня можно вычислить с помощью длины экстраполяции из соотношения [ ср. [39]
Опирающиеся на подшипники фланцы Фл, предотвращают перемещение диска в вертикальном направлении. Будем полагать, что масса и радиус стержня пренебрежимо малы по сравнению соответственно с массой и радиусом диска. Допустим также, что в некоторой точке на расстоянии h от оси к диску приложена внешняя сила F, модуль и направление которой могут, вообще говоря, меняться со временем. [40]
Очевидно, что мы имеем дело с дисперсией волны, так как k ( о / с. Если длина волны очень мала по сравнению с радиусом стержня, то уравнение ( 13), как показал Банкрофт2), переходит в характеристическое уравнение для волн Рэлея в упругом полупространстве. [41]
 |
Значения коэффициентов для вычисления касательных напряжений я угла закручивания для стержня прямоугольного сечения. [42] |
На рис. 11.13, а показана цилиндрическая винтовая пружина. Обозначим: R - радиус пружины; г - радиус стержня пружины; G - модуль сдвига; и - число витков; h - шаг витков пружины. [43]
 |
Сечение пучков стержней с центральным стержнем. [44] |
Поместим начало координат в точку касания стержней. Координаты х и у приведены к безразмерному виду делением на радиус стержня. [45]
Страницы: 1 2 3 4