Безразмерный радиус
Cтраница 1
Безразмерные радиусы каждой из зон приведены ниже. [1]
Безразмерные радиусы каждой из зон даны ниже. [2]
Здесь г0 - безразмерный радиус максшальн or cfn ( площади сечения тела вращения ( для сферы г0 1, а для затупленного, конуса ] г0 1 2), К - р № и / ( ро и) - безразмерный импульс вдуваемого газа. [4]
Напомним, что безразмерный радиус пласта равен единице, область стоков ограничена окружностью, радиус которой равен R, пласт разрабатывается в услориях упруго-водонапорного режима фильтрации. [5]
R rNfa - безразмерный радиус сопла ( rN - радиус сопла); f ( R) - функция безразмерного радиуса сопла для квазистационарного истечения, при котором размер капли определяется равновесием между силами тяжести и силами межфазного натяжения ( см. литературу [25]); Wec Uw2djv ( pc ipA) / 2iCT - критерий Вебера, определяемый через скорость истечения из сопла ( VN) и среднюю плотность фаз, равную ( рс рд) / 2; dN - диаметр отверстия сопла. [6]
Напомним, что безразмерный радиус пласта равен единице, область стоков ограничена окружностью, радиус которой равен R, пласт разрабатывается в условиях упруго-водонапорного режима фильтрации. [7]
При известных значениях безразмерных радиусов сферы Л ] и давления Pso за ударной волной в момент взрыва можно нанести соответствующую им точку на рис. 3.3, а для получения избыточного давления на любом другом расстоянии от центра сферы необходимо из нанесенной точки провести линию, параллельную близлежащей. [8]
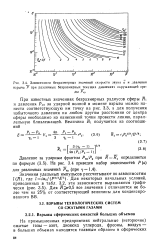 |
Зависимости безразмерных значений скорости звука и и давления взрыва Я при различных безразмерных гекущих давлениях окружающей среды P-sti. [9] |
При известных значениях безразмерных радиусов сферы R и давления Pso за ударной волной в момент взрыва можно нанести соответствующую им точку на рис. 3.3, а для получения избыточного давления на любом другом расстоянии от центра сферы необходимо из нанесенной точки провести линию, параллельную близлежащей. [10]
Здесь через г обозначается безразмерный радиус; Э - полярный угол. [11]
Из этого трансцендентного уравнения находим безразмерные радиусы ядра течения вязко-пластичной среды в затрубном пространстве. При этом, задавшись одним из радиусов, определяем другой радиус течения. [12]
Следовательно, в процессе пластической деформации безразмерный радиус в данной точке изменяется от 1 до некоторого значения г, соответствующего текущему значению приложенных внешних усилий. [13]
Гроне довольно подробно разбирается случай цилиндра безразмерного радиуса, равного единице. [14]
Результаты представлены в форме графиков зависимости безразмерного радиуса от безразмерного времени с безразмерной скоростью в качестве параметра. [15]
Страницы: 1 2 3 4
