Безразмерный радиус

Cтраница 2

Эти кривые построены для случая, когда безразмерный радиус окружности, ограничивающей область стоков, равен 0.2, а суммарный дебит стоков постоянный. Общий вид кривых, изображенных на рис. 2.52 очень похож на соответствующие кривые распределения понижения давления в окрестности точечного стока, работающего в аналогичных условиях. На всех графиках рис. 2.52 видно, что уже при т S 0 8 практически устанавливается постоянное, т.е. стационарное, распределение понижения давления. [16]

Эти кривые построены для случая, когда безразмерный радиус окружности, ограничивающей область стоков, равен 0.2, а суммарный дебит стоков постоянный. Общий вид кривых, изображенных на рис. 2.52 очень похож на соответствующие кривые распределения понижения давления в окрестности точечного стока, работающего в аналогичных условиях. На всех графиках рис. 2.52 видно, что уже при т 0 8 практически устанавливается постоянное, т.е. стационарное, распределение понижения давления. [17]

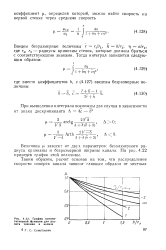График вспомо-гательной функции для расчета течения в канале. [18]

Величина jx зависит от двух параметров: безразмерного радиуса кривизны и безразмерной ширины канала. На рис. 4.22 приведен график этой величины. [19]

На рис, 12 показан характер изменения безразмерного радиуса разгруженной зоны в зависимости от механических свойств горных пород. [20]

Числовые значения f в зависимости от величины безразмерного радиуса частицы хг рассчитаны Генри. [21]

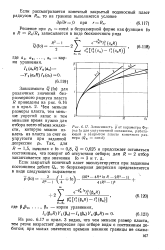Зависимость р от параметра Фурье fo для укрупненной скважины, работающей в закрытом пласте конечного размера ( QB const. [22]

Зависимости Q ( fo) для различных значений безразмерного радиуса пласта R приведены на рис. 6.16 и в прил. Чем меньше размеры пласта, тем меньше упругий запас и тем меньшее время нужно для отбора всего объема жидкости, которую можно извлечь из пласта за счет ее упругости при заданной депрессии рс. [23]

Таким образом, если параметры разряда таковы, что безразмерный радиус кожуха у становится больше 2 8, то шнур оказывается неустойчивым по отношению к извиванию. [24]

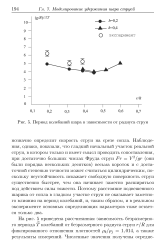Период колебаний шара в зависимости от радиуса струи. [25]

На рис. 5 приведена рассчитанная зависимость безразмерного периода Т колебаний от безразмерного радиуса струи r / R для фиксированного отношения плотностей рь / pj - 1 014, а также результаты измерений. [26]

Из-за сложности полученных расчетных формул в работе [76 ] приведены графики изменения безразмерного радиуса промерзания и тепловых потоков во времени. [27]

Здесь и - скорость внешнего движения; р r / R - безразмерный радиус; х - координата ( безразмерная), отсчитываемая вдоль нулевой линии тока от критической точки. [28]

Как и следовало ожидать, найденное выражение суммы ряда (2.10) в различных интервалах изменения безразмерного радиуса р определяется различными выражениями. [29]

По отношению а0 / тр q % / q из справочных таблиц находят величины безразмерных радиусов q2 и q кругов Мора для одноосного сжатия и растяжения. [30]

Страницы: 1 2 3 4