Радиус-вектор - планета
Cтраница 2
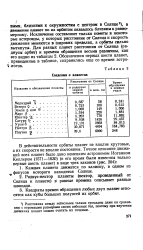 |
Сведения о планетах. [16] |
Радиус-вектор планеты ( вектор, проведенный от Солнца к планете) в равные времена описывает равные площади. [17]
Радиус-вектор планеты, проведенный из Солнца как начала координат, описывает в равные промежутки времени равные площади. [18]
Радиус-вектор планеты описывает в равные времена равные площади. [19]
Кеплера: радиус-вектор планеты описывает равные площади за равные промежутки времени. Следует, однако, подчеркнуть, что постоянство секториальной скорости имеет место при действии любой центральной силы, а не только силы, обратно пропорциональной квадрату расстояния. [20]
Прямая ( радиус-вектор планеты), проходящая от Солнца к планете, описывает равные площади в равные промежутки времени или иначе: секторная скорость планеты остается постоянной величиной в процессе движения. [21]
Прямая ( радиус-вектор планеты), проходящая от Солнца к планете, описывает равные площади в равные промежутки времени, или иначе: секторная скорость планеты остается постоянной в процессе движения. [22]
Определить среднее значение радиус-вектора планеты, если а - большая полуось, а е - эксцентриситет ее эллиптической траектории. [23]
Площади, описываемые радиус-векторами планет относительно Солнца, пропорциональны временам движения планет. [24]
Площади, описываемые радиус-векторами планеты, пропорциональны времени. [25]
Отсюда сразу следует, что на планету действует сила, направленная по радиус-вектору планеты - центральная сила, а орбита ( траектория) - центральная орбита. [26]
Это есть второй закон Кеплера, утверждающий, что за равные промежутки времени радиус-вектор планеты описывает равные площади. [27]
Период обращения по эллипсу равен 2п / п, где среднее движение п представляет среднее по времени значение угловой скорости радиус-вектора планеты; вращаясь равномерно с этой угловой скоростью, радиус-вектор совершает один оборот за период обращения планеты. [28]
Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. Радиус-вектор планеты в равные времена описывает площади одинаковой величины. [29]
Второе из наших уравнений утверждает, что эта скорость постоянна. Этот результат и называется первым законом Кеплера или законом площадей: радиус-вектор планеты описывает в равные промежутки времени равные площади. [30]
Страницы: 1 2 3