Среднелогарифмическая разность - температура
Cтраница 2
На этом графике среднелогарифмическая разность температур и перепад давлений на трубном пучке со стороны первичного контура представлены в функции длины трубы для скоростей воды 6 1; 9 15 и 12 2 м / сек. [16]
В этом случае среднелогарифмическая разность температур рассчитывается так, как если бы теплообменник был противоточным. Поправочные коэффициенты У, которые всегда меньше единицы, обычно приводятся в виде графиков как функции входной и выходной температур и теплоемкостей ( произведений весового расхода и удельной теплоемкости) сред. [17]
При указанной формулировке задачи использование среднелогарифмической разности температур также не вызывает сложностей и трудоемкость расчета примерно такая же, как и при расчете по методу безразмерных характеристик. [18]
Недостаточно обоснован применяемый метод обработки с помощью среднелогарифмической разности температур, составленной из разности температур между материалом и теплоносителем на внешней и внутренней проницаемых поверхностях образцов. При этом в расчете объемного коэффициента теплоотдачи вносится большая погрешность вследствие невозможности точного измерения температуры теплоносителя на входе и выходе из пористой матрицы. [19]
Определить среднелогарифмический температурный напор ( иначе - среднелогарифмическую разность температур) для случая, когда теплообменивающиеся потоки движутся: 1) прямоточно; 2) противоточно; 3) перекрестно; 4) смешанным током, когда поток в межтрубном пространстве делает один ход, а в трубном - два. [20]
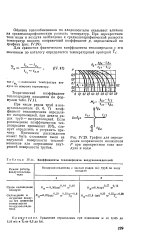 |
График для определения поправочного множителя Р при перекрестном токе воздуха и воды. [21] |
Обвязка теплообменников по хладоносителю оказывает влияние на среднелогарифмическую разность температур. [22]
 |
Изменение температур потоков при противотоке. [23] |
Таким образом, А /, вычисляется как среднелогарифмическая разность температур в начале и конце поверхности теплообмена. [24]
Если при выводе уравнения характеристики теплообменных аппаратов принимается среднелогарифмическая разность температур между греющей и нагреваемой средами, то выражение для расчета коэффициента эффективности Е принимает вид экспоненциальной зависимости. [25]
Для теплообменного аппарата с прямоточной схемой движения теплоносителя среднелогарифмическая разность температуры принимается также в качестве истинного значения средней разности температуры, но она численно существенно меньше, чем для теплообменника с противотоком. [26]
FT - поверхность нагрева теплообменного аппарата; ДТср - среднелогарифмическая разность температур теплоносителя и нагреваемой среды. [27]
Выше уже отмечалось, что расчеты поверхности теплопередачи по среднелогарифмической разности температур дает существенную ошибку. В качестве иллюстрации этого Положения в табл. 5 - 3 приведены расчетные величины логарифмической и истинной разности температур при охлаждении воздуха с давлением 50 и 60 ата тем же весовым количеством обратных газов, уходящих под давлением 1 ата. В таблице также приведены сравнительные данные по - поверхностям теплопередачи, подсчитанным с помощью & ист и & лог. [28]
 |
Тсшюобмонман поверхность А в зависимости от D. параметра Л и длины труб. [29] |
Ограничения раиности температур возникают в связи с возможными отклонениями среднелогарифмической разности температур от идеального значения, которые обусловлены различной организацией потока. [30]
Страницы: 1 2 3 4 5