Абсолютная величина - ошибка
Cтраница 1
 |
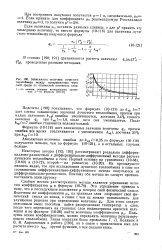
Зависимость величины лучистого теплообмена между поверхностями через слой среды от оптической плотности слоя. [1] |
Абсолютная величина ошибки до & Э ( Ь / 0 25 по формуле ( 10 - 118) получается меньше, чем по формуле ( 10 - 121), а в остальных случаях больше. [2]
 |
Зависимость величины лучистого теплообмена между поверхностями через слой среды от оптической плотности слоя. [3] |
Абсолютная величина ошибки до & Э ( 6 / 0 25 по формуле ( 10 - 118) получается меньше, чем по формуле ( 10 - 121), а в остальных случаях больше. [4]
Абсолютная величина ошибки а называется абсолютной ошибкой. [5]
Равные по абсолютной величине ошибки равновероятны. [6]
Малые по абсолютной величине ошибки более вероятны, нежели большие. [7]
В силу теоремы Лейбница абсолютная величина ошибки, получающейся при замене суммы такого ряда его частичной суммой, не превосходит абсолютной ве личины первого из отброшенных членов. [8]
Использование весового распределения компенсирует изменение абсолютной величины ошибок опыта при измерениях вращения при разных длинах волн. Таким образом, при анализе можно использовать данные в области длин волн от 600 до 185 ммк. Это дает возможность лучше оценивать значения параметров. [9]
В силу известной теоремы Лейбница, абсолютная величина ошибки, получающейся при замене суммы такого ряда его - - частичной суммой, не превосходит абсолютной величины первого из отброшенных членов. [10]
Последний ряд является при любом значении х знакочередующимся, следовательно, абсолютная величина ошибки при замене суммы ряда его частной суммой не превосходит абсолютной величины последнего из удерживаемых членов ряда. [11]
Последний ряд является при любом значении х знакочередующимся, следовательно, абсолютная величина ошибки при замене суммы ряда его частной суммой не превосходит абсолютной величины последнего из удерживаемых членов ряда. [12]
Как показывают результаты обработки измерений, при нагрузке до 5000 н абсолютная величина ошибки среднего арифметического возрастает с увеличением нагрузки, а отношение ошибки среднего арифметического к его значению, характеризующее погрешность силомера, с увеличением нагрузки уменьшается. [13]
Для характеристики ошибок вводят понятие средней арифметической ошибки, равной математическому ожиданию абсолютной величины ошибок. [14]
При определении уровня существенности учитывают, как правило, два фактора: абсолютную величину ошибки и относительную величину ошибки. [15]
Страницы: 1 2 3