Разрезание - граф
Cтраница 2
Стохастический подход к разрезанию графа связан с намеренным введением элемента случайности в процесс разрезания. [16]
Глобальный рандомизированный алго ритм разрезания графов. [17]
Рассмотрим основную идею метода разрезания графа на произвольное число кусков. Минимальное значение числа соединительных ребер для любого графа предлагается находить путем выделения в графе максимально связных кусков. [18]
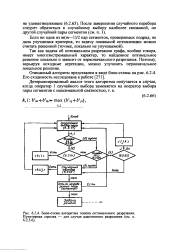 |
Блок-схема алгоритма поиска оптимального разрезания. Пунктирная стрелка - для случая адаптивного разрезания ( п.. [19] |
Так как задача об оптимальном разрезании графа, вообще говоря, имеет многоэкстремальный характер, то найденное оптимальное решение локально и зависит от первоначального разрезания. [20]
Определим теперь число возможных вариантов разрезания графа на куски. [21]
Основное внимание уделяется решению задач разрезания графа схемы на заданное и произвольное число подграфов, размещения графа схемы па плоскости с минимизацией суммарной длины и внутрисхемных пересечений ребер. Исследуются вопросы планарности схем и трассировки соединений. Приводятся программы основных алгоритмов проектирования дискретных устройств, представленные на языке ЛЯПАС. [22]
Рассмотрим работу алгоритма на примере разрезания графа G, показанного на рис. 2.8, на три куска, содержащих соответственно 3, 4 и 5 вершин. [23]
Минимизацию числа соединительных ребер при разрезании графа G на куски будем производить путем последовательной перестановки вершин из одного куска в другой. [24]
Каждая его вершина Q есть множество разрезаний графа G. Для каждой вершины Q определена нижняя граница числа кластеров разрезаний, входящих в вершину Q. [25]
Горин штейн, Метод упорядоченного перебора для разрезания графов. [26]
Если G Gi GI, то процесс разрезания графов на куски закончен. [27]
 |
Расположение внешних аы - [ IMAGE ] Кристалл полупроводниковой БИС водов на кристалле БИС. [28] |
Эти методы позволяют более эффективно решать задачу разрезания графа в тех случаях, когда в подграфах присутствуют группы сильно связанных вершин, которые в процессе оптимизации компоновки следует переставлять одновременно. [29]
Как уже отмечалось, суть итерационных методов разрезания графов схем заключается в выборе первого случайного разрезания с дальнейшими перестановками вершин из одного куска в другой с целью минимизации числа соединительных ребер. [30]
Страницы: 1 2 3 4