Разрезание - граф
Cтраница 3
В предыдущих параграфах рассмотрены последовательные и итерационные алгоритмы разрезания графа схемы на куски, причем число вершин в куске определялось априорно до работы алгоритмов. [31]
Представляет значительный интерес исследовать вопросы, связанные с разрезанием графа на произвольное число кусков с приблизительно одинаковым количеством вершин в каждом куске. Содержательно эту задачу можно трактовать как компоновку модулей в ячейки ( ячеек в панели) с целью получения минимального числа внешних выводов с последующим расположением полученных кусков на стандартных конструктивных единицах. [32]
Легко заметить, что полученная задача не является задачей о разрезании графа - тут ничего не разрезается и не агрегируется. [33]
Именно это обстоятельство заставляет искать стохастические подходы к решению задачи о разрезании графа большой размерности. [34]
Задача об агрегации графа, которую часто называют задачей о сегментации или разрезании графа, довольно широко распространена в приложениях. Содержание ее состоит в следующем. [35]
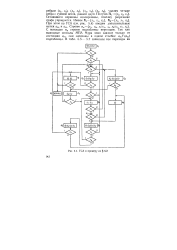 |
ГСА к примеру из §. [36] |
Получим Х1 ха, хэ, я4 - Оставшиеся вершины изолированы, поэтому разрезание графа упрощается. При этом на ГСА ( см. рис. 5.4) вводим дополнительные метки alo и atl. [37]
Вторая глава посвящена решению задачи компоновки элементов схем дискретных устройств, которые решаются путем разрезания графа схемы на подсхемы с минимизацией числа соединительных ребер. Рассматриваются последовательные и итерационные алгоритмы разрезания графов на куски. Приводится методика разрезания графа на квазиминимальные массивы. Дан один из возможных методов покрытия функциональной схемы схемой соединения модулей. [38]
Предположим, что для полного перебора этих решений используется ЭВМ, которая производит один вариант разрезания графа за одну микросекунду. [39]
При медленном изменении среды адаптивная агрегация может быть сведена к последовательному повторению решения задачи о разрезании графа. Именно поэтому задаче адаптивной агрегации графа предшествует задача о его разрезании. [40]
Xcon t, то задача адаптации сводится к оптимизационной задаче (6.2.14), которую обычно называют задачей о разрезании графа. [41]
Вообще говоря, это условие может быть снято, но тогда решаемая задача перестанет быть задачей о разрезании графа, так как некоторые вершины как бы расщепляются в процессе агрегации. [42]
Сложность решения задачи компоновки БИС, определяемой в общем случае выражениями (5.2) - (5.4), зависит от числа N возможных разрезаний графа. [43]
Тогда W ( C) Mans, а многогранники W ( L), W ( К) есть допустимая область соответственно в задаче о линейном размещении графа и в задаче о разрезании графа. Граф многогранника W ( R) является полным. [44]
Поэтому на каждом шаге алгоритма нет необходимости заново строить матрицу В, нужно заменить только такие элементы bhq, у которых либо & - й, либо q - и элемент находится в пере - / ставляемых строках k и 7 - Приведем ЛЯПАС-программу разрезания графа на заданное число кусков с использованием чисел связности по матрице смежности. [45]
Страницы: 1 2 3 4