Неэволюционный разрыв

Cтраница 2

Таким образом, задача о взаимодействии разрыва с малыми возмущениями не имеет решения в линейном приближении. Так как ожидается, что корректно поставленная физическая задача будет иметь решение, это означает, что должны иметь место конечные ( не малые) отклонения от начального состояния. Проведенные ранее исследования различных физических задач показывают, что взаимодействие малых возмущений с неэволюционными разрывами приводит к распаду последних на два или более эволюционных разрыва ( см. гл. [16]

Ву показаны на рис. 5.25 после 200 ( 1) и 6000 ( 2) шагов по времени. Количество расчетных ячеек равно 8000, Ал: 0.5, а число Куранта равно 0.8. Мгновенный распад ударной волны разрежения очевиден, в то время как результирующая структура содержит промежуточную волну, которая должна быть неустойчива к поперечным возмущениям. Видно, что после 6000 шагов по времени от первоначально сформировавшейся составной волны отщепляется неэволюционный разрыв. С течением времени он в конце концов превращается во вращательный разрыв. [17]

Заметим, что в окрестности неэволюционной части ударной адиабаты около точки Е два автомодельных решения могут быть интерпретированы как результат двух вариантов распада неэволюционного разрыва под действием малых возмущений. Эти решения не являются близкими в смысле абсолютного значения их разности, но они остаются близкими в смысле других мер различия, например, учитывающих объем области физического пространства, где эти решения сильно различаются. Это связано с тем обстоятельством, что скорости ударных волн, образующихся в результате распада неэволюционного разрыва, близки к его скорости. [18]

Численные эксперименты показали, что все изменения в неэволюционной ударной волне являются обратимыми даже в тех случаях, в которых осцилляции приводят к очень большим абсолютным значениям / z и волна 2 - 3 становится практически неотличимой от вращательного разрыва. В численном эксперименте это приводит к испусканию периодической медленной волны вместе с другими волнами существенно меньшей амплитуды. Таким образом, если накачивать в неэволюционный скачок возмущения, увеличивающие интеграл / z, то как бы близко мы не приблизились к альфвеновскому разрыву, при обращении знака возмущения опять будет восстанавливаться неэволюционный разрыв того же типа. [19]

Точки, принадлежащие области III, отвечают неэволюционным разрывам, так как имеется слишком много основных соотношений для того, чтобы разрыв мог быть эволюционным, и это положение не может быть улучшено. В определенных случаях, такие разрывы могут состоять из нескольких эволюционных разрывов, движущихся с одинаковой скоростью. Очевидно, малое возмущение может вызвать появление относительной скорости этих разрывов. В таком случае начальный неэволюционный разрыв распадается на эволюционные разрывы, движущиеся с различными скоростями. [20]

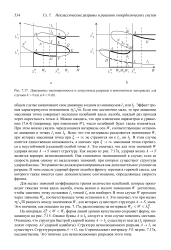Диаграммы эволюционности и допустимые разрывы в композитных материалах для случаев h О ( а и h О ( Ь. [21]

На интервале А W Wj форма линий уровня качественно сохраняет форму, показанную на рис. 7.15. Однако буквы А и / 2 следует в этом случае поменять местами. Структура неэволюционного разрыва А - 1г не существует. Структура разрывав - G, где G принадлежит интервалу FE на рис. 7.17 а, неединственна. Это типично для неэволюционных разрывов этого типа. [22]

Существует еще одно важное обстоятельство. При выводе соотношений (7.2.13) из (7.2.12), для нахождения величин С и С была использована часть равенств (7.2.12), а затем произведена их подстановка в оставшиеся соотношения. Указанные величины могут быть найдены при условии существования соответствующего им ненулевого минора в якобиане, полученном дифференцированием левых частей соотношений (7.2.12) по этим величинам. Очевидно, этот случай отвечает неэволюционным разрывам. [23]

Wt, причем считалось, что иа стремятся к конечным пределам при % - оо. При k О существование решений, отвечающих разрывам, принадлежащим отрезку ЕК ударной адиабаты было доказано аналитически. В серии численных расчетов было показано, что структура всегда существует для всех эволюционных ударных волн. Таким образом, эти исследования не позволяют отбросить какую-либо часть ударных волн как нереализуемую. В то же самое время среди априорно неэволюционных разрывов, не было найдено допустимых разрывов. [24]

Это контактный разрыв, но с той разницей, что помимо разрыва плотности в нем имеется еще разрыв тангенциальной компоненты скорости. Разрыв касательной, тангенциальной компоненты скорости невозможен в ударной волне; но если нормальная компонента скорости равна нулю и отсутствует скачок давления, то, как легко проверить, разрыв тангенциальной скорости допускается условиями сохранения трех потоков. Тангенциальный разрыв характеризуется двумя параметрами - скачками плотности и тангенциальной скорости. Таким образом, минимальный набор стандартных разрывов, на которые может распасться произвольный неэволюционный разрыв рассматриваемой природы, содержит две ударные волны и один тангенциальный разрыв ( Ландау и Лиф-шиц ( 1953)): ударные волны движутся друг от друга по разные стороны первоначального разрыва, а на месте последнего остается тангенциальный разрыв. [25]

Путем численного эксперимента было показано, что структуры неэволюционных ударных волн могут быть довольно устойчивыми к расщеплению под действием альфвеновских возмущений. Они могут поглощать эти возмущения, меняя или свою внутреннюю структуру, если она описывается свободным параметром, или интенсивность. Неэволюционная ударная волна может также расщепиться на эволюционную ударную волну и неэволюционную волну другого типа. Количество альфвеновских возмущений, необходимых чтобы это произошло, зависит от величины диссипативных коэффициентов, определяющих толщину структуры, а следовательно, от возможности неэволюционной ударной волны абсорбировать приходящие возмущения. В пределе исчезающей диссипации достаточно бесконечно малого альфвеновского возмущения, для того чтобы сделать неэволюционный разрыв неотличимым от вращательного. В этом смысле полученные в вышеупомянутых работах результаты не противоречат классическим результатам, относящимся к идеальной магнитной газовой динамике. Исключение могли бы составить такие случаи, в которых, по мере того как диссипативные коэффициенты стремятся к нулю, все более и более жесткие ограничения накладываются на малость приходящих альфвеновских возмущений. [26]

Неэволюционные разрывы, очевидно, не могут быть стационарными; со временем они распадаются на некоторые стандартные разрывы, удовлетворяющие необходимым условиям сохранения. При этом в каждом случае формируется набор стандартных разрывов, обеспечивающий, так сказать, согласование состояний среды по обе стороны поверхности разрыва. Под скоростью v здесь нужно понимать ( как и в § 5.2) нормальную, а под скоростью vt - тангенциальную к поверхности разрыва компоненту скорости. Между этими величинами в общем случае не существует никаких связей, они вполне произвольны, так как при столкновении приходят в соприкосновение две массы газа, сжатые до различных плотностей и давлений и имеющие различные нормальные и тангенциальные к поверхности соприкосновения скорости. Поэтому для стандартного перехода от состояния 1 к состоянию 2 необходимо располагать четырьмя произвольными параметрами, что и определяет число стандартных разрывов, образующихся после распада неэволюционного разрыва. [27]

МГД-уравнений для идеальной, бесконечно проводящей плазмы, показано, что она имеет гиперболический тип, и выписана невырожденная система собственных векторов матрицы ее коэффициентов. Как упоминалось ранее, решения гиперболических систем в общем случае должны содержать разрывы. Это, конечно, справедливо также и для уравнений магнитной гидродинамики. Поэтому должны развиваться численные методы решения МГД-системы, записанной в консервативной форме. Эта система включает в себя интегральные законы сохранения массы, импульса и энергии с учетом действия электромагнитных сил и дополняется уравнениями Максвелла, описывающими поведение электромагнитного поля. Последняя подсистема в магнитогидродинамическом приближении также может быть записана в форме законов сохранения. Для полноты изложения в разд. МГД-уравнений, и указаны те из них, которые удовлетворяют свойству эволюционности. Отдельно обсуждается вопрос об эволюционности параллельных ударных волн и волн включения и выключения. МГД-задачи Римана в одномерной постановке. Приводятся также результаты тестовых расчетов, позволяющие сделать заключение о предпочтительности использования тех или иных разновидностей TVD-схем годуновского типа. Эти особенности связаны с наличием схемных вязкости и сопротивления, которые неизбежно возникают при использовании конечно-разностных и конечно-объемных методов. Присутствие численной диссипации может затормозить распад неэволюционных разрывов или их комбинаций, который в идеальном случае происходит мгновенно под действием бесконечно малого возмущения. Так как схемная вязкость зависит от выбора расчетной сетки и, естественно, от выбора самого численного метода, время расщепления неэволюционного разрыва на эволюционные оказывается схемно-зависимым. Роу, основанного на решении линеаризованной задачи о распаде произвольного разрыва, на МГД-задачи, содержащие сильное фоновое магнитное поле. [28]

Страницы: 1 2