Контактный разрыв

Cтраница 3

Измерение длительности бесконтактной паузы производится для каждого контактного разрыва. [31]

Пусть оси декартовой системы координат у элемента контактного разрыва выбраны так, что ( 3) совпадает с нормалью, а ( л:) и ( Х2) лежат в касательной плоскости к разрыву. [32]

Измерению подвергается весь токоведущий контур, а также контактные разрывы каждой камеры и отделителя в отдельности. [33]

В первой из них в каждую сторону от контактного разрыва по газу распространяются ударные волны. Во второй конфигурации в одну сторону распространяется ударная волна, в другую-центрированная волна Римана. Наконец, в третьей конфигурации в обе стороны от контактного разрыва распространяются центрированные волны Римана. Во всех случаях между расходящимися волнами образуется область постоянных значений давления и скорости газа, включающая контактную поверхность, на которой в общем случае терпит разрыв плотность газа. [34]

Между волнами образуется два постоянных течения, разделенных контактным разрывом, на котором давление и массовая скорость непрерывны, а плотность, температура, энтропия и другие термодинамические величины, как правило, разрывны. [35]

При X - 0 они непрерывным образом вырождаются в контактные разрывы в среде частиц. [36]

Выясним, являются ли эволюционными изученные ранее разрывы - контактные разрывы, ударные волны, волны детонации и волны дефлаграции. [37]

Наибольшие трудности существуют при расчете переноса, когда возникают контактные разрывы. [38]

Известно, что схемы более высокого порядка лучше рассчитывают контактные разрывы. Поэтому в отличие от расчета насыщенности для численного решения уравнения переноса может оказаться перспективным использование схем повышенного порядка точности. Однако применение известных схем второго порядка точности ( Лакса-Вендроффа, Кранка-Никольсона и других) приводит, в силу их немонотонности, к появлению значительных осцилляции, а введение псевдовязкости заметно снижает точность решений. Этим же недостатком обладают алгоритмы метода конечных элементов. [39]

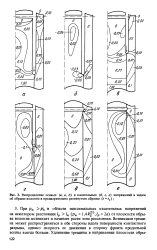Распределение осевых ( а, в, д и касательных ( б, г, е напряжений в задаче об обрыве волокна в предварительно растянутом образце ( t tQ. [40]

Возникшая трещина может распространяться в обе стороны вдоль поверхности контактного разрыва, однако скорость ее движения в сторону фронта продольной волны всегда больше. [41]

Количественный анализ показывает, что в обратном направлении от контактного разрыва по газу может распространяться как ударная волна, так и волна разрежения. [42]

Возможность использования решения задачи об отражении ударной волны от контактного разрыва лишь в области слева от сечения 0 при изменении условий справа от этого сечения в задаче об отражении волны от открытого конца трубы основана на том, что в двух последних случаях изменение условий справа от сечения х0 не влияет на течение газа слева от него, поскольку все характеристические скорости в сечении х0 положительны ( с 0 в случае рис. 2.13.6, б); в первом же случае условие, соответствующее открытому концу трубы, удовлетворено. [43]

Рассмотрим, наконец, пересечение скачка уплотнения с поверхностью контактного разрыва. [44]

Рассмотрим некоторые задачи о течениях с ударными волнами и контактными разрывами и покажем, как эти задачи могут быть решены методом характеристик. [45]

Страницы: 1 2 3 4