Раскачка - колебание
Cтраница 1
Раскачка колебаний, как видно из решения задачи 3.5.32 сопро-вождается биениями. При со - со0 размах биений неограниченно растет, но зато их период, а значит, и время нарастания неограниченно увеличиваются. Пусть время, прошедшее после начала воздействия вынуждающей силы, много меньше 2тг / со - со0 I - Воспользуйтесь приближением sine v e ( е 1) и определите характер раскачки колебаний в этом случае. [1]
Раскачка колебаний вторичным пучком должна быть наиболее эффективна на границе второго и третьего этапов, где ток вторичных электронов максимален. Из расчетов, аналогичных тем, которые были сделаны при обсуждении результатов ( 37 ], следует, что на границе второго и третьего этапов горит разряд, инициируемый вторичным электронным пучком. Существование данной неустойчивости в [23] объяснили тем, что плотность плазмообразующего газа вблизи поверхности металла определяется конкуренцией между подачей и расходом газа, а зажигание разряда увеличивает отток газа, поскольку ионы, движущиеся из разрядной области, имеют большую скорость по сравнению с нейтральными атомами. В [37] в условиях, близких к условиям [27], при использовании методов скоростной фоторегистрации наблюдали пульсации плазменного факела, поэтому можно сделать предположение, что в [27] пульсации тока мишени и давления газа обусловлены пульсациями плотности приповерхностной плазмы. Более того, можно предположить, что механизм этих пульсаций обусловлен неустойчивостью горения разряда за счет упоминавшегося выше эффекта ионной откачки. Однако непосредственное использование механизма ионной откачки для объяснения колебательной неустойчивости в [27] наталкивается на ряд трудностей. Поэтому скорость иоиов больше скорости нейтралов, причем в режиме ионной откачки поток ионов может на порядок превосходить поток подводимого в камеру плазмообразующего газа. Колебательная же неустойчивость в [27] развивается несколько в других условиях. Во-первых, в [27] отсутствует вблизи поверхности металла сильное продольное магнитное поле, поэтому ионы, как и нейтральные частицы, могут совершенно беспрепятственно уходить на стенки вакуумной камеры. [2]
Раскачка колебаний, как видно из решения задачи 3.5.32 сопро-вождается биениями. При со - оо размах биений неограниченно растет, но зато их период, а значит, и время нарастания неограниченно увеличиваются. Пусть время, прошедшее после начала воздействия вынуждающей силы, много меньше 2тг / 1 со - - со0 I - Воспользуйтесь приближением sin е ъ е 1) и определите характер раскачки колебаний в этом случае. [3]
Раскачка колебаний, как видно из результатов задачи 5.31, сопровождается биениями. При со-со 0 размах биений растет, но зато их период, а значит, и время нарастания неограниченно увеличиваются. [4]
Раскачка колебаний в плазме направленным потоком частиц в некотором смысле аналогична раскачке морских волн под действием ветра, однако с тем существенным различием, что обычный ветер вызывает волнение на поверхности моря, а электрический ветер в плазме создает волны объемного типа. [5]
Раскачка колебаний может произойти от различных нарушений термодинамического равновесия. При кинетической неустойчивости такое нарушение касается распределения частиц по скоростям. Можно ожидать раскачки и из-за неравновесного распределения в пространстве, например из-за неравномерной температуры, но этот вопрос подробно еще не исследован. [6]
При we0 первоначальная раскачка колебаний с амплитудой почти со t плавно уменьшается и устанавливаются вынужденные колебания. [7]
Аномальное затухание и раскачка колебаний в плазме могут рассматриваться как проявления эффекта Вавилова - Черепкова. [8]
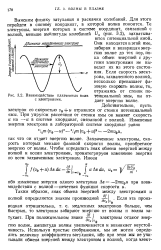 |
Взаимодействие плазменных волн тенциальной ЯМЫ, он От-с электронами. дает энергию. [9] |
Выясним физику затухания и раскачки колебаний. Для этого перейдем в систему координат, в которой волна покоится. Те электроны, энергия которых в системе координат, связанной с волной, меньше амплитуды колебаний С / ( рис. 3.2), захватываются потенциальной ямой. Они находятся в этой яме, забирая и возвращая энергию волне до тех пор, пока обмен энергией с другими электронами не выведет их из этого состоя-х ния. [10]
Fo с т ПРИ раскачке колебаний диффузия в пространстве скоростей должна идти в сторону расплывания функции распределения по А, и при этом в силу сохранения адиабатического инварианта должна уменьшаться средняя поперечная энергия частиц. [11]
Предел сжатию орбит накладывается раскачкой колебаний, обусловленной квантовым характером излучения: потеря энергии электрона на излучение происходит отд. [12]
Неустойчивость Бунемана связана с раскачкой колебаний ионов за счет взаимодействия ионов с пучком электронов. При этом мы считаем, что разброс электронов по скоростям мал по сравнению со скоростью электронного пучка. [13]
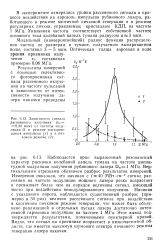 |
Зависимость сигнала рассеянного излучения ( А 3 0 44 мкм от частоты модуляции Q в режиме повторяющихся импульсов ч ( / и в пич-ковом режиме ( 2. [14] |
Наблюдается ярко выраженный резонансный характер раскачки колебаний капель тумана на частоте амплитудной модуляции излучения рубинового лазера QM1 МГц. Вертикальными отрезками обозначен разброс результатов измерений. Измерения показали, что начиная с / 40 МВт-см-2 сигнал рассеяния на частоте модуляции мощного лазера резко возрастает и превышает более чем на порядок величины сигнал, имеющий место при воздействии немодулированного излучения. Начиная с указанного порога, наблюдается существенный разброс ( примерно в 30 раз) величин рассеянного сигнала при воздействии в хаотичном пичковом режиме генерации, что может быть объяснено реализацией в отдельных пусках лазера достаточно интенсивной гармоники модуляции на частоте 1 МГц. Этот вывод подтверждается результатами, помеченными пунктирной кривой. Видно, что сигнал на приемнике возрастает в низкочастотной области, где имеется максимум шумового спектра пичкового режима генерации лазера накачки. [15]
Страницы: 1 2 3 4