Раскраска - вершина
Cтраница 2
Свойства квазиполных графов позволяют предложить практические алгоритмы раскраски вершин графа. [16]
В задаче о раскраске графа требуется найти способ раскраски вершин графа в несколько цветов ( занумерованных целыми числами) таким образом, чтобы любые две соседние вершины были покрашены в различные цвета. Принятие решения заключается в том, чтобы установить, можно ли покрасить вершины в С или меньше цветов с соблюдением указанного требования, а оптимизация - в том, чтобы найти минимально необходимое число цветов. [17]
К задачам вложения графов может быть отнесена задача раскраски вершин графа. Граф G называют К-раскрашиваемым, если существует такое разбиение множества его вершин на К непересекающихся подмножеств, что ребра в G соединяют вершины только из разных подмножеств. Если каждому подмножеству взаимно однозначно поставить в соответствие краску, то граф G не содержит смежных вершин, окрашенных одной краской. Таким образом, согласно определению полного А - дольного графа, задача раскраски графа G в К красок есть задача вложения графа G в полный А-дольный граф. [18]
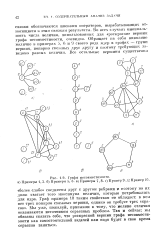 |
Графы несовместимости, а Примеры 1, 2. б Примеры 5, 6. в Примеры 7, 8. г Пример 9. д Пример 10. [19] |
Во всех случаях минимальность числа величин, использованных для раскраски вершин графа несовместимости, очевидна. Обращает на себя внимание наличие в примерах 5, 6 и 9 своего рода ядер в графах - групп вершин, попарно смежных друг другу и поэтому требующих заведомо разных величин. [20]
Из этого результата следует, что любой теореме о раскраске вершин планарного графа соответствует двойственная теорема о раскраске граней карты, и наоборот. [21]
 |
Кубы с четырьмя вершинами каждого цвета. [22] |
Для иллюстрации теоремы мы приводим на рис. 4.6.2 шесть способов раскраски вершин куба Q3, отвечающих тому случаю, когда в кубе имеется по четыре вершины каждого цвета. Заметим, что ожерелья, изображенные на рис. 2.4.2, соответствуют в точности булевым функциям от двух переменных, ибо всякое допустимое преобразование ожерелья с четырьмя бусинками можно заменить соответствующим преобразованием на 2-кубе. [23]
Нужно показать, что Я ( п) цветов достаточно для раскраски вершин графа G. Если же рН ( п), то подставим Н ( п) вместо р в (12.10) и произведем алгебраические преобразования. [24]
А Завершая эту главу, бросим беглый тоскующий взгляд на проблему раскраски вершин. В этом параграфе мы свяжем с каждым графом некоторую функцию, которая, помимо всего прочего, будет содержать информацию о том, является граф 4-раскрашиваемым или нет. [25]
При решении задач обработки информации и управления в распределенных системах, требующих раскраски вершин графов, большое значение приобретают оценки его хроматического числа. [26]
 |
Граф G [ IMAGE ] Колесо W7. [27] |
Первое, что необходимо изменить в ГА - это замена бинарной ЦФ на ЦФ раскраски вершин. Согласно ЦФ выбираем первый ген ( вершину) в хромосоме и присваиваем ей первый реальный цвет, если это возможно. [28]
Минимизация выражения (4.14) обеспечивает выполнимость следующего условия: цвет / 1 не будет использован в раскраске вершин, если цвета от 1 до; достаточны для допустимой раскраски. & ], которая дает решение приведенной выше задачи линейного 0 - 1-программирования, определяет оптимальную раскраску, а используемое при этом число цветов равно хроматическому числу графа. [29]
Минимизация выражения (4.14) обеспечивает выполнимость следующего условия: цвет / 1 не будет использован в раскраске вершин, если цвета от 1 до / достаточны для допустимой раскраски. [30]
Страницы: 1 2 3 4