Раскраска - вершина
Cтраница 3
В шестой главе исследуются оптимизационные задачи на графах, такие как задачи разбиения, размещения, раскраски вершин графов, нахождения пути коммивояжера, построения деревьев Штейнера, трассировки соединений, построения клик, независимых подмножеств, покрывающих деревьев, определения планарности и изоморфизма графов. Для решения указанных задач применяются различные методы ЭМ. Рассмотрены нечеткие модифицированные алгоритмы их решения. Описаны итерационные методы парных и групповых перестановок, методы последовательного приближения, релаксации, поиска в глубину и ширину, направленного перебора и другие, а также эвристики, использующие различные методы статистической оптимизации. Эти эвристики представлены методами отжига, генетического поиска и их модификациями. Применяется группировка сильно связанных вершин в кластеры с дальнейшим сбором этих кластеров в заданные части разбиения, а также использование фрактальных множеств для группирования сильно связанных вершин. Рассмотрены последовательный ГА разбиения, алгоритм разбиения графов на части на основе модифицированной агрегации фракталов. Проанализировано использование итерационного разбиения гиперграфа и ГА дихотомического разбиения графа. При решении проблем разбиения графов на части рассмотрены задачи группирования элементов, обладающих одинаковыми свойствами. [31]
Было доказано, что наименьшее число цветов, достаточное для раскраски ребер любого графа без петель с максимальной степенью ст, равно [ За / 2 ], а для раскраски вершин любого графа без петель и кратных ребер достаточно о 1 цветов. [32]
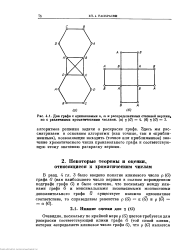 |
Два графа с одинаковыми п, т в распределениями степеней вершин, но с различными хроматическими числами, ( а у ( б 4. ( б у ( б 2. [33] |
Здесь мы рассматриваем в основном алгоритмы ( как точные, так и приближенные), позволяющие находить ( точное или приближенное) значение хроматического числа произвольного графа и соответствующую этому значению раскраску вершин. [34]
Опять-таки автор может рассчитывать, что часть читателей, прочитав условие задачи экономии памяти в этой формулировке, усмотрит в пей прямую связь со знаменитой задачей теории графов - задачей о раскраске вершин графа: надо раскрасить вершины графа в наименьшее число красок так, чтобы никакая пара смежных вершин не оказалась раскрашенной одной краской. Этот факт сам по себе очень интересен, но сейчас мы не будем отвлекаться, а опять вернемся к нашему примеру. [35]
Эффективность сети автоматизации проектирования, производства и эксплуатации современных систем во многом определяется оптимальностью распределенного банка данных, размещенного в блоках памяти сети, при этом многие оптимизационные задачи сводятся к раскраске вершин графа. При решении этих задач большое значение приобретают оценки хроматического числа графа. [36]
Раскраски вершин S2 и S7 совпадают по второй компоненте. Поскольку раскраски вершин S5 и S2 также совпадают по второй компоненте, то для переходов, взвешенных входным вектором Х3, недетерминированности не возникает. Таким образом, данная многокомпонентная раскраска определяет кодирование внутренних состояний автомата в 3-значном структурном алфавите, при котором элементы памяти функционально несвязны. [37]
Для графов большой размерности процедура выделения всех порожденных циклов нечетной длины становится затруднительной. При реализации практических алгоритмов раскраски вершин графов может быть использована специальная процедура, позволяющая выделять порожденные циклы, не превышающие заданной длины. Проведенный машинный эксперимент, основанный на раскраске случайно порождаемых графов, показал, что учет распределения порожденных циклов длины более девяти практически не влияет на точность получаемого решения. [38]
Выделим из графа Г / максимальный подграф Г, ни одна пара вершин которого ее соединена ребром. Эта задача может быть решена раскраской вершин графа Гу, при которой любые две смежные вершины окрашиваются в разные цвета и число i) i вершин, окрашенных в первый цвет, максимально возможно. Поскольку любые две выходные переменные у, и у /, соответствующие вершинам подграфа Гу, никогда одновременно не равны единице, значения каждой из них могут быть сформированы на выходах одного дешифратора. [39]
Тот или иной способ изображения молекулярного графа определяется характером задачи, которая решается с его помощью. Каждый из трех способов позволяет с учетом раскраски вершин и ребер однозначно восстановить два других, поскольку число и типы функциональных групп исходных мономеров известны из их строения. [40]
Правильная вершинная ( реберная) раскраска - это раскраска вершин ( ребер) графа, при к-рой любые смежные вершины ( ребра) окрашены в разные цвета. Правильную вершинную раскраску часто наз. Наименьшее число цветов, достаточное для правильной вершинной раскраски графа G, наз. [41]
Каждому покрытию семантической таблицы соответствует одна или несколько многокомпонентных раскрасок графа сцепления в три краски. Среди раскрасок выбираем такую, в которой совпадению значений компонент раскрасок вершин, коин-цидентных ребрам, составляющим покрытие, соответствует совпадение значений компонент раскрасок вершин, в которые осуществляется переход под действием входных векторов, взвешивающих ребра графа сцепления, вошедшие в покрытие. [42]
Строим двудольный граф G ( V, V), где Уесть множество вершин для G, a V - множество из k цветов. Для любого конечного множества FcV определяется выбирающая функция при помощи такой раскраски вершин графа G ( F), что соединенные ребром вершины имеют различные цвета. [43]
Строим двудольный граф G ( V, V), где V есть множество вершин для G, a V - множество из k цветов. Для любого конечного множества F с: V определяется выбирающая функция при помощи такой раскраски вершин графа G ( F), что соединенные ребром вершины имеют различные цвета. [44]
 |
Два различных стереоизомера, изображающиеся одним и тем же молекулярным графом.| Различные изомеры степени полимеризации I 4 ( тетрамеры. [45] |
Страницы: 1 2 3 4