Расположение - координатная ось
Cтраница 3
На рис. 1 изображены проекции контактных линий для различных фаз зацепления архимедовой червячной передачи на плоскость XOZ, параллельную осям червяка и червячного колеса, и на плоскость YOZ, перпендикулярную к оси червяка. Расположение координатных осей выбрано так, что ось ОХ совпадает с осью червяка, а ось OY-с линией кратчайшего расстояния между осями червяка и червячного колеса. [31]
Выбираем сначала расположение координатных осей X, У. Разделяем фигуру на прямоугольники, центры тяжести С, Сг, Сг которых находятся в точках пересечения диагоналей каждого из них. [32]
 |
Комбинированная автоматически закрывающаяся масленка с.| Игольчатая маслодозировка. [33] |
На основе игольчатой маслодозировки в НИИЧАСПРОМе сконструирован и изготовлен полуавтомат для одновременной смазки значительного числа деталей часов. Прибор при соответствующем изменении расположения координатных осей может также применяться для смазки других точных механизмов. [34]
Описывают точечные группы, выделяя из стереографической проекции элементов симметрии группы минимальный сферический треугольник, повторением которого в пространстве в результате воздействия этих элементов симметрии можно получить всю точечную группу. Однозначность описания точечных групп требует стандартизации расположения координатных осей в пространстве кристалла. Обычно ось г располагают вдоль главной оси, а оси х и у по возможности совмещают с осями 2 или 2, перпендикулярными главной оси. Стандартная установка приведена в табл. 2.2 и на рис. 2.7. Понятно, что эта стандартная установка единственно возможна только в кристаллах кубической системы. Множественностью установок кристалла объясняются часто разночтения в справочной литературе о структу - pax конкретных фаз. [35]
Правило знаков для изгибающего момента установлено независимо от направления координатных осей, вторая же производная, как известно, положительна, если в сторону положительной оси у обращена вогнутость кривой, и отрицательна, - если выпуклость ( фиг. Таким образом, знак изгибающего момента М ( х) не зависит от расположения координатных осей; знак же второй производной - зависит. [36]
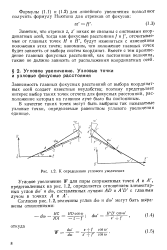 |
К определению углового увеличения. [37] |
Заметим, что отрезки г, г никак не связаны с системами координатных осей, тогда как фокусные расстояния / и /, отсчитываемые от главных точек Н и / /, будут изменяться с изменением положения этих точек; напомним, что положение главных точек будет зависеть от выбора систем координат. Вместе с тем произведение главных фокусных расстояний, как постоянная величина, также не должно зависеть от расположения координатных осей. [38]
При построении аксонометрических проекций пирамиды на рис. 474 и 475 мы сохранили углы между аксонометрическими осями и аксонометрические масштабы. Об этом следует помнить при решении вопроса об изменении расположения координатных осей в пространстве. [39]
Далее находим кривую ( Л) и область ( А) в плоскости uv, находящиеся во взаимно однозначном соответствии с кривой ( L) и ограниченной ею областью. Предполагая теперь, что плоскость uv снабжена ориентацией, отвечающей расположению координатных осей и и v [ см. 548 ], мы можем определить знак направления обхода контура ( L) в зависимости от выбранной стороны поверхности ( S) следующим образом. [40]
В соответствии с элементами симметрии кристаллов они по структуре подразделяются принадлежностью к той или иной кристаллической системе, или так называемой сингонии. Известно семь основных кристаллических систем. Принадлежность кристалла к той или иной системе определяется относительной величиной и расположением координатных осей, мысленно проведенных внутри кристалла. Каждой кристаллической системе соответствуют две формы - призматическая и бипирамидальная. [41]
Введенное нами понятие длины волны и полученное уравнение луча остаются в силе и для продольных колебаний. В этом случае под х следует понимать расстояние от источника до положения равновесия колеблющейся точки М, а под у - смещение этой же точки от положения равновесия. Поскольку для продольных волн у параллельно х, то для этого случая расположение координатных осей на графиках рис. 4.20 и 4.21 следует считать чисто условным и не соответствующим их реальному расположению в пространстве. [42]
Введенное нами понятие длины волны и полученное уравнение луча остаются в силе и для продольных колебаний. В этом случае под х следует понимать расстояние от источника до положения равновесия колеблющейся точки М, а под у - смещение этой же точки от положения равновесия. Поскольку для продольных воли у параллельно х, то для этого случая расположение координатных осей на графиках рис. 4.20 и 4.21 следует считать чисто условным и не соответствующим их реальному расположению в пространстве. [43]
Введенное нами понятие длины волны и полученное уравнение луча остаются в силе и для продольных колебаний. В этом случае под х следует понимать расстояние от источника до положения равновесия колеблющейся точки М, а под у - смещение этой же точки от положения равновесия. Поскольку для продольных волн у параллельно х, то для этого случая расположение координатных осей на графиках рис. 4.20 и 4.21 следует считать чисто условным и не соответствующим их реальному расположению в пространстве. [44]
При вычислении координат его вершин наиболее удобно поместить начало декартовой системы координат в центре фигуры, координатную ось Z направить параллельно боковым ребрам трехгранной призмы АВСА В С, а ось Т - параллельно ребрам АА2, ВЕ2, СС2 гептаэдроида. Что касается осей X и Y, то они располагаются в плоскости, параллельной треугольнику основания ЛВС, причем X, как и в большинстве предыдущих фигур, перпендикулярно, а У параллельно стороне АВ. Расположение координатных осей, их положительные и отрицательные направления указаны на фиг. Как и ранее, принимаем, что все ребра гептаэдроида равны между собой и каждое равно двум. [45]
Страницы: 1 2 3 4